Wing Weight Function#

import numpy as np
import matplotlib.pyplot as plt
import uqtestfuns as uqtf

The Wing Weight test function [FSK08] is a 10-dimensional scalar-valued function. The function has been used as a test function in the context of metamodeling [ZZP+20] and optimization [FSK08].

Test function instance#

To create a default instance of the wing weight test function:

my_testfun = uqtf.WingWeight()

Check if it has been correctly instantiated:

print(my_testfun)

Name              : WingWeight
Spatial dimension : 10
Description       : Wing weight model from Forrester et al. (2008)

Description#

The weight of a light aircraft wing is computed using the following analytical expression:

\[ \mathcal{M}(\boldsymbol{x}) = 0.036 \, S_w^{0.758} \, W_{fw}^{0.0035} \, \left( \frac{A}{\cos^2{(\Lambda)}} \right)^{0.6} q^{0.006} \lambda^{0.04} \left(\frac{100 t_c}{\cos{(\Lambda)}}\right)^{-0.3} \left( N_z W_{dg} \right)^{0.49} + S_w W_p \]

where \(\boldsymbol{x} = \{ S_w, W_{fw}, A, \Lambda, q, \lambda, t_c, N_z, W_{dg}, W_p\}\) is the vector of input variables defined below.

Probabilistic input#

Based on [FSK08], the probabilistic input model for the Wing Weight function consists of eight independent uniform random variables with ranges shown in the table below.

my_testfun.prob_input

Name: Wing-Weight-Forrester-2008

Spatial Dimension: 10

Description: Probabilistic input model for the Wing Weight model from Forrester et al. (2008).

Marginals:

No. Name Distribution Parameters Description
1 Sw uniform [150. 200.] wing area [ft^2]
2 Wfw uniform [220. 300.] weight of fuel in the wing [lb]
3 A uniform [ 6. 10.] aspect ratio [-]
4Lambda uniform [-10. 10.] quarter-chord sweep [degrees]
5 q uniform [16. 45.] dynamic pressure at cruise [lb/ft^2]
6lambda uniform [0.5 1. ] taper ratio [-]
7 tc uniform [0.08 0.18] aerofoil thickness to chord ratio [-]
8 Nz uniform [2.5 6. ] ultimate load factor [-]
9 Wdg uniform [1700 2500] flight design gross weight [lb]
10 Wp uniform [0.025 0.08 ] paint weight [lb/ft^2]

Copulas: None

Reference Results#

This section provides several reference results of typical UQ analyses involving the test function.

Sample histogram#

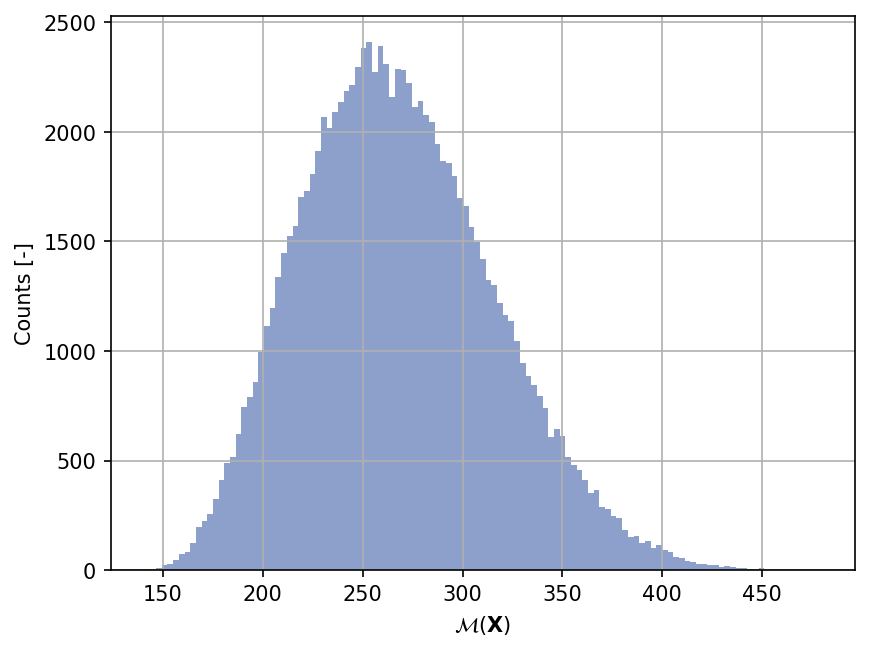
Shown below is the histogram of the output based on \(100'000\) random points:

np.random.seed(42)
xx_test = my_testfun.prob_input.get_sample(100000)
yy_test = my_testfun(xx_test)

plt.hist(yy_test, bins="auto", color="#8da0cb");
plt.grid();
plt.ylabel("Counts [-]");
plt.xlabel("$\mathcal{M}(\mathbf{X})$");
plt.gcf().set_dpi(150);
../_images/wing-weight_9_0.png

Moments estimation#

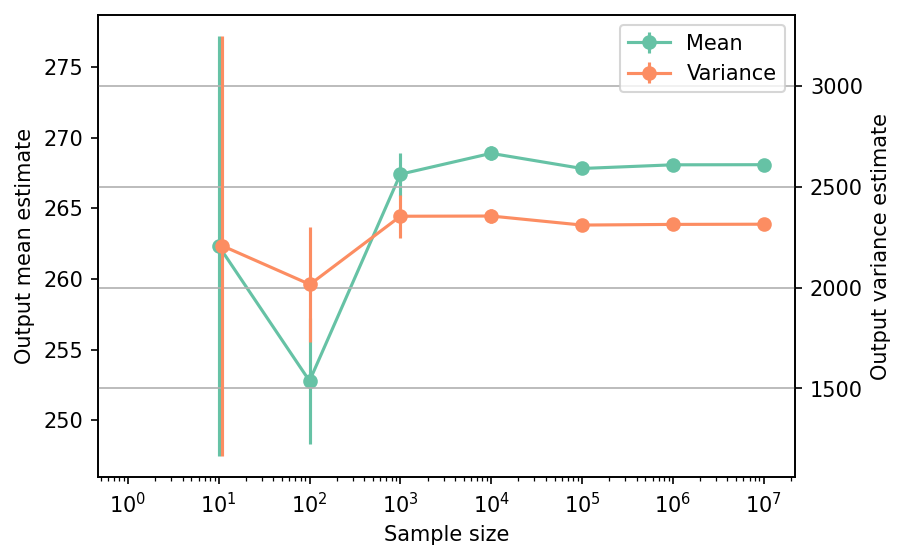
Shown below is the convergence of a direct Monte-Carlo estimation of the output mean and variance with increasing sample sizes.

# --- Compute the mean and variance estimate
np.random.seed(42)
sample_sizes = np.array([1e1, 1e2, 1e3, 1e4, 1e5, 1e6, 1e7], dtype=int)
mean_estimates = np.empty(len(sample_sizes))
var_estimates = np.empty(len(sample_sizes))

for i, sample_size in enumerate(sample_sizes):
    xx_test = my_testfun.prob_input.get_sample(sample_size)
    yy_test = my_testfun(xx_test)
    mean_estimates[i] = np.mean(yy_test)
    var_estimates[i] = np.var(yy_test)

# --- Compute the error associated with the estimates
mean_estimates_errors = np.sqrt(var_estimates) / np.sqrt(np.array(sample_sizes))
var_estimates_errors = var_estimates * np.sqrt(2 / (np.array(sample_sizes) - 1))

# --- Do the plot
fig, ax_1 = plt.subplots(figsize=(6,4))

ax_1.errorbar(
    sample_sizes,
    mean_estimates,
    yerr=mean_estimates_errors,
    marker="o",
    color="#66c2a5",
    label="Mean",
)
ax_1.set_xlabel("Sample size")
ax_1.set_ylabel("Output mean estimate")
ax_1.set_xscale("log");
ax_2 = ax_1.twinx()
ax_2.errorbar(
    sample_sizes + 1,
    var_estimates,
    yerr=var_estimates_errors,
    marker="o",
    color="#fc8d62",
    label="Variance",
)
ax_2.set_ylabel("Output variance estimate")

# Add the two plots together to have a common legend
ln_1, labels_1 = ax_1.get_legend_handles_labels()
ln_2, labels_2 = ax_2.get_legend_handles_labels()
ax_2.legend(ln_1 + ln_2, labels_1 + labels_2, loc=0)

plt.grid()
fig.set_dpi(150)
../_images/wing-weight_11_0.png

The tabulated results for each sample size is shown below.

from tabulate import tabulate

# --- Compile data row-wise
outputs = []
for (
    sample_size,
    mean_estimate,
    mean_estimate_error,
    var_estimate,
    var_estimate_error,
) in zip(
    sample_sizes,
    mean_estimates,
    mean_estimates_errors,
    var_estimates,
    var_estimates_errors,
):
    outputs += [
        [
            sample_size,
            mean_estimate,
            mean_estimate_error,
            var_estimate,
            var_estimate_error,
            "Monte-Carlo",
        ],
    ]

header_names = [
    "Sample size",
    "Mean",
    "Mean error",
    "Variance",
    "Variance error",
    "Remark",
]

tabulate(
    outputs,
    headers=header_names,
    floatfmt=(".1e", ".4e", ".4e", ".4e", ".4e", "s"),
    tablefmt="html",
    stralign="center",
    numalign="center",
)
Sample size Mean Mean error Variance Variance error Remark
1.0e+01 2.6234e+02 1.4853e+01 2.2062e+03 1.0400e+03 Monte-Carlo
1.0e+02 2.5279e+02 4.4892e+00 2.0153e+03 2.8645e+02 Monte-Carlo
1.0e+03 2.6741e+02 1.5339e+00 2.3530e+03 1.0528e+02 Monte-Carlo
1.0e+04 2.6889e+02 4.8518e-01 2.3540e+03 3.3293e+01 Monte-Carlo
1.0e+05 2.6782e+02 1.5196e-01 2.3093e+03 1.0328e+01 Monte-Carlo
1.0e+06 2.6807e+02 4.8090e-02 2.3126e+03 3.2705e+00 Monte-Carlo
1.0e+07 2.6808e+02 1.5210e-02 2.3135e+03 1.0347e+00 Monte-Carlo

References#

FSK08(1,2,3)

Alexander I. J. Forrester, András Sóbester, and Andy J. Keane. Engineering Design via Surrogate Modelling: A Practical Guide. Wiley, 1 edition, 2008. ISBN 978-0-470-06068-1 978-0-470-77080-1. doi:10.1002/9780470770801.

ZZP+20

Lavi R. Zuhal, Kemas Zakaria, Pramudita S. Palar, Koji Shimoyama, and Rhea P. Liem. Gradient-enhanced universal Kriging with polynomial chaos as trend function. In AIAA Scitech 2020 Forum. Orlando, Florida, 2020. American Institute of Aeronautics and Astronautics. doi:10.2514/6.2020-1865.