Tutorial: Create a Custom Test Function
Contents
Tutorial: Create a Custom Test Function#
You may add an uncertainty quantification (UQ) test functions to UQTestFuns such that they share the same interface like the built-in ones. There are two ways to add a new test function to UQTestFuns:
Interactively within a given Python session; if not saved, the test function will be gone after a new session.
Updating the package by implementing the function in a new module within the UQTestFuns package; the test function will available after importing the package.
In this tutorial, you’ll learn how to add a test function interactively. If you want to add a new test function as a Python module, please refer to the relevant section in the Developer’s Guide.
import numpy as np
import uqtestfuns as uqtf
Uncertainty quantification test functions revisited#
In essence, an uncertainty quantification (UQ) test function contains the following components:
an evaluation function that takes inputs and produces outputs; we can think of such functions as a blackbox
a probabilistic input model that specifies the input to the blackbox function as a joint random variable; the results of a UQ analysis depend on this specification
(optionally) a set of parameters that completes the test function specification; these parameters once set are kept during the function evaluation (for example, flag, numerical tolerance, and time-step size).
When defining a new generic UQ test function, it’s a good idea to think about the candidate test function in those three terms and be ready with their specifications.
Branin function#
Suppose we want to add the two-dimensional Branin (or Branin-Hoo) function as a test function [1]. The function is defined analytically as follows:
where \(x_1\) and \(x_2\) are the input variables and \(\{ a, b, c, r, s, t \}\) are the parameters.
The input variables are defined in the table below.
No. |
Name |
Distribution |
Parameters |
|---|---|---|---|
1 |
\(x_1\) |
uniform |
\([-5, 10]\) |
2 |
\(x_2\) |
uniform |
\([0, 15]\) |
The typical values for the parameters are shown in the table below.
No. |
Parameter |
Value |
|---|---|---|
1 |
\(a\) |
\(1.0\) |
2 |
\(b\) |
\(\frac{5.1}{(2 \pi)^2}\) |
3 |
\(c\) |
\(\frac{5}{\pi}\) |
4 |
\(r\) |
\(6\) |
5 |
\(s\) |
\(10\) |
6 |
\(t\) |
\(\frac{1}{8 \pi}\) |
Evaluation function#
The first component of a test function is the evaluation function itself. UQTestFuns requires for such a function to have at least the input array as its first parameter. When applicable, the parameters must be the second parameter of the function. The Branin evaluation function can be defined as a Python function as follows:
def evaluate_branin(xx: np.ndarray, params: np.ndarray):
"""Evaluate the Branin function on a set of input values.
Parameters
----------
xx : np.ndarray
2-Dimensional input values given by an N-by-2 array where
N is the number of input values.
params : np.ndarray
The parameters of the Branin function;
a 1-Dimensional array of length 5.
Returns
-------
np.ndarray
The output of the Branin function evaluated on the input values.
The output is a 1-dimensional array of length N.
"""
yy = (
params[0] * (xx[:, 1] - params[1] * xx[:, 0]**2 + params[2] * xx[:, 0] - params[3])**2
+ params[4] * (1 - params[5]) * np.cos(xx[:, 0])
+ params[4]
)
return yy
Input and parameters#
The second and third components of a test function are
the (probabilistic) input specification and the parameters.
The input specification of the Branin function consists of
two independent uniform random variables with different bounds.
In UQTestFuns, a probabilistic input model is represented by ProbInput class
and an instance of it can be defined as follows:
# Define a list of marginals
marginals = [
uqtf.UnivDist(distribution="uniform", parameters=[-5, 10], name="x1"),
uqtf.UnivDist(distribution="uniform", parameters=[0, 15], name="x2"),
]
# Create a probabilistic input
my_input = uqtf.ProbInput(marginals=marginals, name="Branin-Input")
To verify if the instance has been created successfully, print it out to the terminal:
print(my_input)
Name : Branin-Input
Spatial Dim. : 2
Description : None
Marginals :
No. Name Distribution Parameters Description
----- ------ -------------- ------------ -------------
1 x1 uniform [-5 10]
2 x2 uniform [ 0 15]
Copulas : None
Finally, the parameters of the Branin function defined above can be defined as a NumPy array as follows:
my_params = np.array([1.0, 5.1 / (2 * np.pi)**2, 5 / np.pi, 6, 10, 1 / (8 * np.pi)])
Note
The parameters can practically be of any Python data type. They only depend on how they are going to be consumed by the specified evaluation function. In other words, you have full control on how to define the parameters.
Creating a test function#
The evaluation function, probabilistic input, and parameters are combined
to make a test function via the UQTestFun class.
An instance of the class for the Branin function is written as follows:
my_testfun = uqtf.UQTestFun(
evaluate=evaluate_branin,
prob_input=my_input,
parameters=my_params,
name="Branin function",
)
Print the resulting instance to the terminal to verify:
print(my_testfun)
Name : Branin function
Spatial dimension : 2
Congratulations! You’ve successfully created a test function instance of the Branin function inside a Python session. This instance can be evaluated as a usual function. Below are the surface and contour plots of the test function; both require function evaluation on the grid.
import matplotlib.pyplot as plt
from mpl_toolkits.axes_grid1 import make_axes_locatable
# --- Create a 2-D grid
xx_1 = np.linspace(
my_input.marginals[0].lower, my_input.marginals[0].upper, 2000
)
xx_2 = np.linspace(
my_input.marginals[1].lower, my_input.marginals[1].upper, 2000
)
mesh_2d = np.meshgrid(xx_1, xx_2)
xx_2d = np.array(mesh_2d).T.reshape(-1, 2)
yy_2d = my_testfun(xx_2d)
# --- Create the plots
fig = plt.figure(figsize=(11, 5))
# Surface
axs_1 = plt.subplot(121, projection='3d')
axs_1.plot_surface(
mesh_2d[0],
mesh_2d[1],
yy_2d.reshape(2000, 2000).T,
cmap="plasma",
linewidth=0,
antialiased=False,
alpha=0.5
)
axs_1.set_xlabel("$x_1$", fontsize=14)
axs_1.set_ylabel("$x_2$", fontsize=14)
axs_1.set_zlabel("$\mathcal{M}(x_1, x_2)$", fontsize=14)
# Contour
axs_2 = plt.subplot(122)
cf = axs_2.contourf(
mesh_2d[0], mesh_2d[1], yy_2d.reshape(2000, 2000).T, 20, cmap="plasma"
)
axs_2.set_xlabel("$x_1$", fontsize=14)
axs_2.set_ylabel("$x_2$", fontsize=14)
divider = make_axes_locatable(axs_2)
cax = divider.append_axes('right', size='5%', pad=0.05)
fig.colorbar(cf, cax=cax, orientation='vertical')
axs_2.axis('scaled')
# Optimum value locations
axs_2.scatter(
np.array([-np.pi, np.pi, 9.42478]), np.array([12.275, 2.275, 2.475]),
s=80,
marker="x",
color="white"
)
fig.tight_layout(pad=3.0)
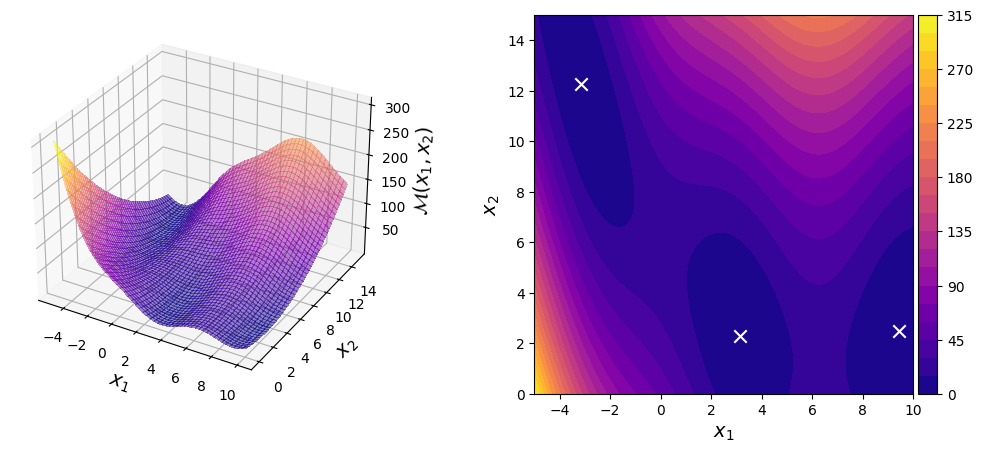
The Branin function is a test function typically used for testing optimization algorithms. Shown in the contour plot above are the locations of the three global optima of the function.
Concluding remarks#
The test function created above only persists in the current Python session. To use the same Branin test function in another session, you can either repeat the same procedure (for example, via a script) or save it into an object in the disk and load it in the new session.
Alternatively, you can extend UQTestFuns directly by specifying
the test function inside its own module.
This way, once UQTestFuns is loaded you can construct the test function
like any other built-in test function.
For example, if you somehow name the test function Branin then:
my_testfun = uqtf.Branin()
will construct an instance of the Branin function using the default input and parameter values.
You can find a guide on how to do this in more detail in the relevant section of the Developer’s Guide.
- 1
L. C. W. Dixon and G. P. Szegö. Towards global optimization 2, chapter The global optimization problem: an introduction, pages 1–15. North-Holland, Amsterdam, 1978.

