Flood Model
Contents
Flood Model#
import numpy as np
import matplotlib.pyplot as plt
import uqtestfuns as uqtf
The flood model is an eight-dimensional scalar valued function. The model was used in the context of sensitivity analysis in [IL15, LIPG13] and has become a canonical example of the OpenTURNS package [BDIP17].
Test function instance#
To create a default instance of the flood model:
my_testfun = uqtf.Flood()
Check if it has been correctly instantiated:
print(my_testfun)
Name : Flood
Spatial dimension : 8
Description : Flood model from Iooss and Lemaître (2015)
Description#
The flood model computes the maximum annual underflow of a river using the following analytical formula:
where \(\boldsymbol{x} = \{ q, k_s, z_v, z_m, h_d, c_b, l, b \}\) is the eight-dimensional vector of input variables further defined below. The output is given in \([\mathrm{m}]\). A negative value indicates that an overflow (flooding) occurs.
Note
Compared to the original function, this implementation inverted the sign of the output such that underflowing has a positive sign.
The model is based on a simplification of the one-dimensional hydro-dynamical equations of St. Venant under the assumption of uniform and constant flow rate and a large rectangular section.
Probabilistic input#
Based on [IL15] (Table 4), the probabilistic input model for the flood model consists of eight independent random variables with marginals shown in the table below.
my_testfun.prob_input
Name: Flood-Iooss2015
Spatial Dimension: 8
Description: Probabilistic input model for the Flood model from Iooss and Lemaître (2015).
Marginals:
| No. | Name | Distribution | Parameters | Description |
|---|---|---|---|---|
| 1 | Q | trunc-gumbel | [1013. 558. 500. 3000.] | Maximum annual flow rate [m^3/s] |
| 2 | Ks | trunc-normal | [30. 8. 15. inf] | Strickler coefficient [m^(1/3)/s] |
| 3 | Zv | triangular | [49. 51. 50.] | River downstream level [m] |
| 4 | Zm | triangular | [54. 56. 55.] | River upstream level [m] |
| 5 | Hd | uniform | [7. 9.] | Dyke height [m] |
| 6 | Cb | triangular | [55. 56. 55.5] | Bank level [m] |
| 7 | L | triangular | [4990. 5010. 5000.] | Length of the river stretch [m] |
| 8 | B | triangular | [295. 305. 300.] | River width [m] |
Copulas: None
Reference results#
This section provides several reference results of typical UQ analyses involving the test function.
Sample histogram#
Shown below is the histogram of the output based on \(100'000\) random points:
np.random.seed(42)
xx_test = my_testfun.prob_input.get_sample(100000)
yy_test = my_testfun(xx_test)
plt.hist(yy_test, bins="auto", color="#8da0cb");
plt.grid();
plt.ylabel("Counts [-]");
plt.xlabel("$\mathcal{M}(\mathbf{X})$");
plt.gcf().set_dpi(150);
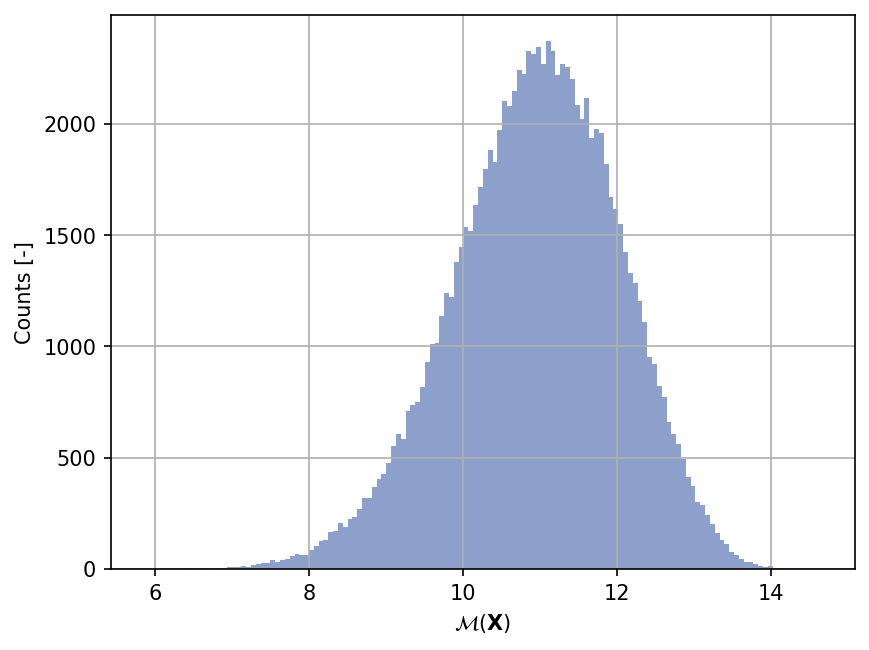
Moments estimation#
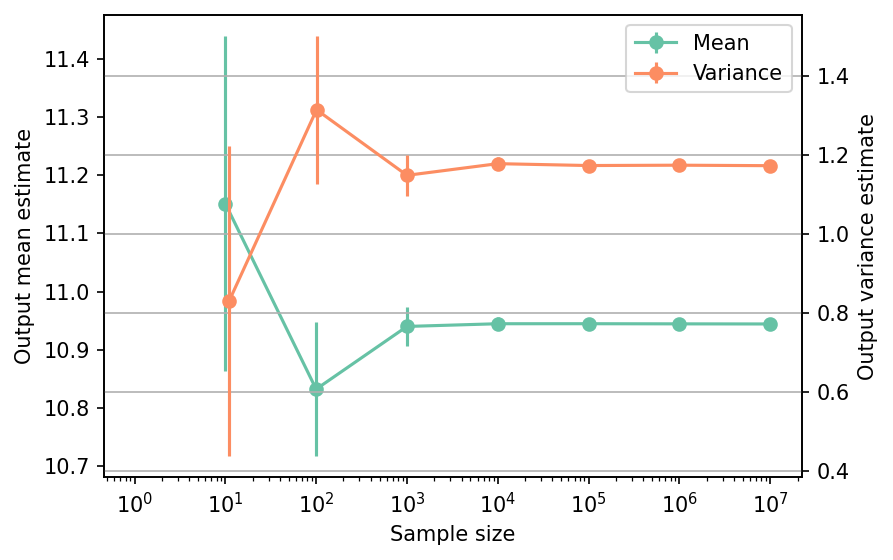
Shown below is the convergence of a direct Monte-Carlo estimation of the output mean and variance with increasing sample sizes.
# --- Compute the mean and variance estimate
np.random.seed(42)
sample_sizes = np.array([1e1, 1e2, 1e3, 1e4, 1e5, 1e6, 1e7], dtype=int)
mean_estimates = np.empty(len(sample_sizes))
var_estimates = np.empty(len(sample_sizes))
for i, sample_size in enumerate(sample_sizes):
xx_test = my_testfun.prob_input.get_sample(sample_size)
yy_test = my_testfun(xx_test)
mean_estimates[i] = np.mean(yy_test)
var_estimates[i] = np.var(yy_test)
# --- Compute the error associated with the estimates
mean_estimates_errors = np.sqrt(var_estimates) / np.sqrt(np.array(sample_sizes))
var_estimates_errors = var_estimates * np.sqrt(2 / (np.array(sample_sizes) - 1))
# --- Do the plot
fig, ax_1 = plt.subplots(figsize=(6,4))
ax_1.errorbar(
sample_sizes,
mean_estimates,
yerr=mean_estimates_errors,
marker="o",
color="#66c2a5",
label="Mean",
)
ax_1.set_xlabel("Sample size")
ax_1.set_ylabel("Output mean estimate")
ax_1.set_xscale("log");
ax_2 = ax_1.twinx()
ax_2.errorbar(
sample_sizes + 1,
var_estimates,
yerr=var_estimates_errors,
marker="o",
color="#fc8d62",
label="Variance",
)
ax_2.set_ylabel("Output variance estimate")
# Add the two plots together to have a common legend
ln_1, labels_1 = ax_1.get_legend_handles_labels()
ln_2, labels_2 = ax_2.get_legend_handles_labels()
ax_2.legend(ln_1 + ln_2, labels_1 + labels_2, loc=0)
plt.grid()
fig.set_dpi(150)
The tabulated results for each sample size is shown below.
from tabulate import tabulate
# --- Compile data row-wise
outputs = []
for (
sample_size,
mean_estimate,
mean_estimate_error,
var_estimate,
var_estimate_error,
) in zip(
sample_sizes,
mean_estimates,
mean_estimates_errors,
var_estimates,
var_estimates_errors,
):
outputs += [
[
sample_size,
mean_estimate,
mean_estimate_error,
var_estimate,
var_estimate_error,
"Monte-Carlo",
],
]
header_names = [
"Sample size",
"Mean",
"Mean error",
"Variance",
"Variance error",
"Remark",
]
tabulate(
outputs,
headers=header_names,
floatfmt=(".1e", ".4e", ".4e", ".4e", ".4e", "s"),
tablefmt="html",
stralign="center",
numalign="center",
)
| Sample size | Mean | Mean error | Variance | Variance error | Remark |
|---|---|---|---|---|---|
| 1.0e+01 | 1.1151e+01 | 2.8825e-01 | 8.3090e-01 | 3.9169e-01 | Monte-Carlo |
| 1.0e+02 | 1.0832e+01 | 1.1468e-01 | 1.3151e+00 | 1.8692e-01 | Monte-Carlo |
| 1.0e+03 | 1.0940e+01 | 3.3899e-02 | 1.1492e+00 | 5.1418e-02 | Monte-Carlo |
| 1.0e+04 | 1.0945e+01 | 1.0857e-02 | 1.1787e+00 | 1.6670e-02 | Monte-Carlo |
| 1.0e+05 | 1.0945e+01 | 3.4263e-03 | 1.1739e+00 | 5.2500e-03 | Monte-Carlo |
| 1.0e+06 | 1.0944e+01 | 1.0839e-03 | 1.1748e+00 | 1.6615e-03 | Monte-Carlo |
| 1.0e+07 | 1.0944e+01 | 3.4258e-04 | 1.1736e+00 | 5.2484e-04 | Monte-Carlo |
References#
- IL15(1,2)
Bertrand Iooss and Paul Lemaître. A review on global sensitivity analysis methods. In Uncertainty Management in Simulation-Optimization of Complex Systems, pages 101–122. Springer US, 2015. doi:10.1007/978-1-4899-7547-8_5.
- BDIP17
Michaël Baudin, Anne Dutfoy, Bertrand Iooss, and Anne-Laure Popelin. OpenTURNS: an industrial software for uncertainty quantification in simulation. In Handbook of Uncertainty Quantification, pages 2001–2038. Springer International Publishing, 2017. doi:10.1007/978-3-319-12385-1_64.
- LIPG13
M. Lamboni, B. Iooss, A.-L. Popelin, and F. Gamboa. Derivative-based global sensitivity measures: General links with Sobol' indices and numerical tests. Mathematics and Computers in Simulation, 87:45–54, 2013. doi:10.1016/j.matcom.2013.02.002.

