Bratley et al. (1992) B function#

import numpy as np
import matplotlib.pyplot as plt
import uqtestfuns as uqtf

The Bratley et al. (1992) B function (or Bratley1992b function for short), is an \(M\)-dimensional scalar-valued function. The function was introduced in [BFN92] as a test function for multi-dimensional numerical integration using low discrepancy sequences.

Note

There are four other test functions used in Bratley et al. [BFN92]:

The function was reintroduced in [SSobol95] with additional parameters for global sensitivity analysis purposes. The “generalized” function became known as the Sobol’-G.

The plots for one-dimensional and two-dimensional Bratley1992b functions are shown below.

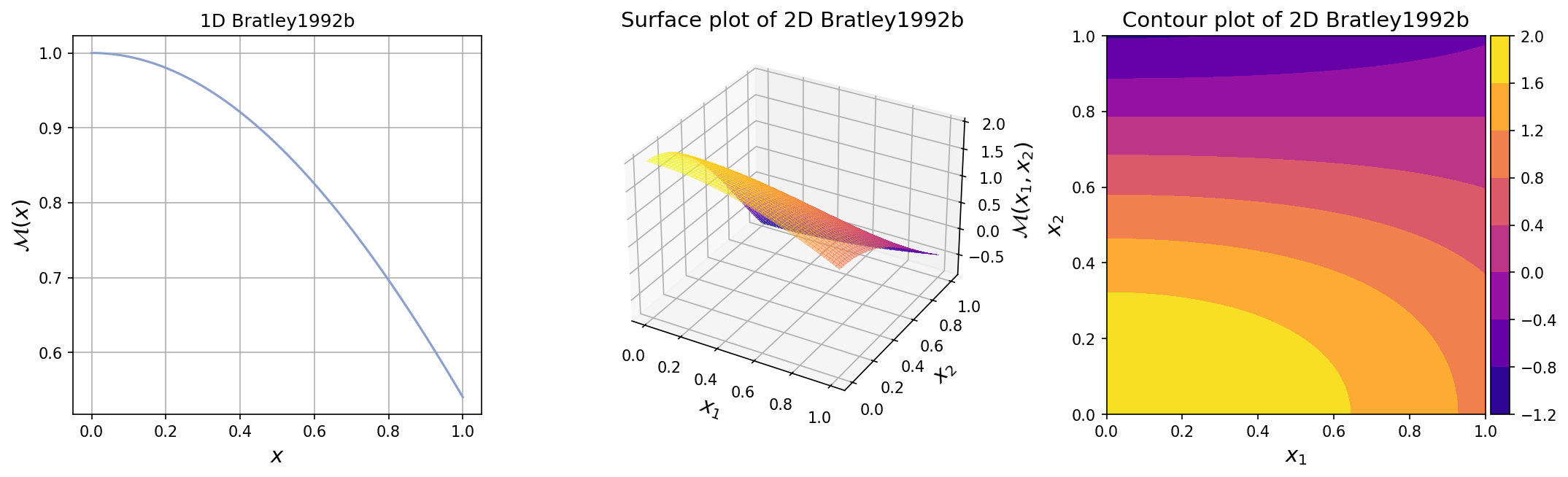
../_images/bratley1992b_3_0.png

Test function instance#

To create a default instance of the test function:

my_testfun = uqtf.Bratley1992b()

Check if it has been correctly instantiated:

print(my_testfun)

Name              : Bratley1992b
Spatial dimension : 2
Description       : Integration test function #2 from Bratley et al. (1992)

By default, the spatial dimension is set to \(2\)1. To create an instance with another value of spatial dimension, pass an integer to the parameter spatial_dimension (keyword only). For example, to create an instance of 10-dimensional Bratley1992b function, type:

my_testfun = uqtf.Bratley1992b(spatial_dimension=10)

Description#

The Bratley1992b function is defined as follows2:

\[ \mathcal{M}(\boldsymbol{x}) = \prod_{m = 1}^{M} m \cos{(m x_m)}, \]

where \(\boldsymbol{x} = \{ x_1, \ldots, x_M \}\) is the \(M\)-dimensional vector of input variables further defined below.

Probabilistic input#

Based on [BFN92], the test function is integrated over the hypercube domain of \([0, 1]^M\). Such an input specification can be modeled using an \(M\) independent uniform random variables as shown in the table below.

No.

Name

Distribution

Parameters

Description

1

\(x_1\)

uniform

[0.0 1.0]

N/A

\(\vdots\)

\(\vdots\)

\(\vdots\)

\(\vdots\)

\(\vdots\)

M

\(x_M\)

uniform

[0.0 1.0]

N/A

Reference results#

This section provides several reference results of typical UQ analyses involving the test function.

Definite integration#

The integral value of the function over the domain of \([0.0, 1.0]^M\) is analytical:

\[ I[\mathcal{M}] (M) \equiv \int_{[0, 1]^M} \mathcal{M}(\boldsymbol{x}) \; d\boldsymbol{x} = \prod_{m = 1}^M \sin{(m)}. \]

The table below shows the numerical values of the integral for several selected dimensions.

Dimension

\(I[\mathcal{M}]\)

1

\(8.4147098 \times 10^{-1}\)

2

\(7.6514740 \times 10^{-1}\)

3

\(1.0797761 \times 10^{-1}\)

4

\(-8.1717723 \times 10^{-2}\)

5

\(7.8361108 \times 10^{-2}\)

6

\(-2.1895308 \times 10^{-2}\)

7

\(-1.4384924 \times 10^{-2}\)

8

\(-1.4231843 \times 10^{-2}\)

9

\(-5.8652056 \times 10^{-3}\)

10

\(3.1907957 \times 10^{-3}\)

The absolute value of the integral is monotonically decreasing function of the number of dimensions. Asymptotically, it is zero. In the original paper of Bratley [BFN92], the integration was carried out for the function in dimension eight.

Moments#

The moments of the test function are analytically known and the first two moments are given below.

Expected value#

Due to the domain being a hypercube, the above integral value over the domain is the same as the expected value:

\[ \mathbb{E}[\mathcal{M}](M) = \prod_{m = 1}^M \sin{(m)}. \]

Variance#

The analytical value for the variance is given as follows:

\[ \mathbb{V}[\mathcal{M}](M) = \frac{1}{4} \prod_{m = 1}^M m (2 m + \sin{(2m)}) - \left( \prod_{m = 1}^M \sin{m} \right)^2. \]

The table below shows the numerical values of the variance for several selected dimensions.

Dimension

\(I[\mathcal{M}]\)

1

\(1.9250938 \times 10^{-2}\)

2

\(5.9397772 \times 10^{-1}\)

3

\(5.0486051 \times 10^{0}\)

4

\(4.5481851 \times 10^{1}\)

5

\(5.3766707 \times 10^{2}\)

6

\(9.245366 \times 10^{3}\)

7

\(2.4253890 \times 10^{5}\)

8

\(7.6215893 \times 10^{6}\)

9

\(2.9579601 \times 10^{8}\)

10

\(1.5464914 \times 10^{10}\)

The variance grows as the number of dimensions and becomes unbounded for a very large dimension.

References#

SSobol95

Andrea Saltelli and Ilya M. Sobol'. About the use of rank transformation in sensitivity analysis of model output. Reliability Engineering & System Safety, 50(3):225–239, 1995. doi:10.1016/0951-8320(95)00099-2.

BFN92(1,2,3,4,5)

Paul Bratley, Bennett L. Fox, and Harald Niederreiter. Implementation and tests of low-discrepancy sequences. ACM Transactions on Modeling and Computer Simulation, 2(3):195–213, 1992. doi:10.1145/146382.146385.

1

This default dimension applies to all variable dimension test functions. It will be used if the spatial_dimension argument is not given.

2

see Section 5.1, p. 207 (test function no. 2) in [BFN92].