Tutorial: Create Built-in Test Functions#

UQTestFuns includes a wide range of test functions from the uncertainty quantification community; these functions are referred to as the built-in test functions. This tutorial provides you with an overview of the package; you’ll learn about the built-in test functions, their common interfaces, as well as their important properties and methods.

By the end of this tutorial, you’ll be able to create any test function available in UQTestFuns and access its basic but important functionalities.

UQTestFuns is designed to work with minimal dependency within the numerical Python ecosystem. At the very least, UQTestFuns requires NumPy and SciPy to work. It might be a good idea to import NumPy alongside UQTestFuns:

import numpy as np
import uqtestfuns as uqtf

Listing available test functions#

To list all the test functions currently available:

uqtf.list_functions()

 No.            Constructor            Dimension                Application                Description
-----  -----------------------------  -----------  --------------------------------------  ----------------------------------------------------------------------------
            Ackley()                  M             optimization, metamodeling        Optimization test function from Ackley (1987)
         Alemazkoor20D()             20                    metamodeling               High-dimensional low-degree polynomial from Alemazkoor & Meidani (2018)
         Alemazkoor2D()               2                    metamodeling               Low-dimensional high-degree polynomial from Alemazkoor & Meidani (2018)
           Borehole()                 8             metamodeling, sensitivity         Borehole function from Harper and Gupta (1983)
         Bratley1992a()               M              integration, sensitivity         Integration test function #1 from Bratley et al. (1992)
         Bratley1992b()               M              integration, sensitivity         Integration test function #2 from Bratley et al. (1992)
         Bratley1992c()               M              integration, sensitivity         Integration test function #3 from Bratley et al. (1992)
         Bratley1992d()               M              integration, sensitivity         Integration test function #4 from Bratley et al. (1992)
       CantileverBeam2D()             2                    reliability                Cantilever beam reliability problem from Rajashekhar and Ellington (1993)
       CircularPipeCrack()            2                    reliability                Circular pipe under bending moment from Verma et al. (2015)
       ConvexFailDomain()             2                    reliability                Convex failure domain problem from Borri and Speranzini (1997)
         DampedCosine()               1                    metamodeling               One-dimensional damped cosine from Santner et al. (2018)
       DampedOscillator()             8             metamodeling, sensitivity         Damped oscillator model from Igusa and Der Kiureghian (1985)
  DampedOscillatorReliability()       8                    reliability                Performance function from Der Kiureghian and De Stefano (1990)
             Flood()                  8             metamodeling, sensitivity         Flood model from Iooss and Lemaître (2015)
         Forrester2008()              1             optimization, metamodeling        One-dimensional function from Forrester et al. (2008)
          FourBranch()                2                    reliability                Series system reliability from Katsuki and Frangopol (1994)
            Franke1()                 2                    metamodeling               (1st) Franke function from Franke (1979)
            Franke2()                 2                    metamodeling               (2nd) Franke function from Franke (1979)
            Franke3()                 2                    metamodeling               (3rd) Franke function from Franke (1979)
            Franke4()                 2                    metamodeling               (4th) Franke function from Franke (1979)
            Franke5()                 2                    metamodeling               (5th) Franke function from Franke (1979)
            Franke6()                 2                    metamodeling               (6th) Franke function from Franke (1979)
           GaytonHat()                2                    reliability                Two-Dimensional Gayton Hat function from Echard et al. (2013)
         Gramacy1DSine()              1                    metamodeling               One-dimensional sine function from Gramacy (2007)
          HyperSphere()               2                    reliability                Hyper-sphere bound reliability problem from Li et al. (2018)
           Ishigami()                 3                    sensitivity                Ishigami function from Ishigami and Homma (1991)
           McLainS1()                 2                    metamodeling               McLain S1 function from McLain (1974)
           McLainS2()                 2                    metamodeling               McLain S2 function from McLain (1974)
           McLainS3()                 2                    metamodeling               McLain S3 function from McLain (1974)
           McLainS4()                 2                    metamodeling               McLain S4 function from McLain (1974)
           McLainS5()                 2                    metamodeling               McLain S5 function from McLain (1974)
          OTLCircuit()                6             metamodeling, sensitivity         Output transformerless (OTL) circuit model from Ben-Ari and Steinberg (2007)
           Oakley1D()                 1                    metamodeling               One-dimensional function from Oakley and O'Hagan (2002)
            Piston()                  7             metamodeling, sensitivity         Piston simulation model from Ben-Ari and Steinberg (2007)
          Portfolio3D()               3                    sensitivity                Simple portfolio model from Saltelli et al. (2004)
         RSCircularBar()              2                    reliability                RS problem as a circular bar from Verma et al. (2016)
          RSQuadratic()               2                    reliability                RS problem w/ one quadratic term from Waarts (2000)
            SobolG()                  M              sensitivity, integration         Sobol'-G function from Saltelli and Sobol' (1995)
       SpeedReducerShaft()            5                    reliability                Reliability of a shaft in a speed reducer from Du and Sudjianto (2004)
            Sulfur()                  9             metamodeling, sensitivity         Sulfur model from Charlson et al. (1992)
           Webster2D()                2                    metamodeling               2D polynomial function from Webster et al. (1996).
           Welch1992()               20       metamodeling, sensitivity, integration  20-Dimensional function from Welch et al. (1992)
          WingWeight()               10             metamodeling, sensitivity         Wing weight model from Forrester et al. (2008)

This function produces a list of test functions, their respective constructor, spatial dimension, typical applications, as well as a short description.

A Callable instance#

Take, for instance, the borehole function [HG83], an eight-dimensional test function typically used in the context of metamodeling and sensitivity analysis. To instantiate a borehole test function, call the constructor as follows:

my_testfun = uqtf.Borehole()

To verify whether the instance has been created, print it to get some basic information on the terminal:

print(my_testfun)

Name              : Borehole
Spatial dimension : 8
Description       : Borehole function from Harper and Gupta (1983)

The resulting object is a Callable. The instance can be evaluated with a set of input values. For example, the eight-dimensional borehole function can be evaluated at a single point (1-by-8 array):

xx = np.array([
  [
    1.04803586e-01, 2.54527756e+03, 9.44572869e+04, 9.94988176e+02,
    6.31793993e+01, 7.63308791e+02, 1.57530252e+03, 1.00591588e+04
  ]
])
my_testfun(xx)

array([50.7642835])

Note

Calling the function on a set of input values automatically verifies the correctness of the input (its dimensionality and bounds). Moreover, the test function accepts a vectorized input (that is, an \(N\)-by-\(M\) array where \(N\) and \(M\) are the number of points and dimensions, respectively)

Probabilistic input#

In general, the results of uncertainty quantification (UQ) analyses depend on the specified probabilistic input. When a test function appears in the literature, a specification for the probabilistic input is usually provided. In UQTestFuns, a probabilistic input model is an integral part of each test function.

For instance, the borehole function has a probabilistic input model that consists of eight independent random variables. This input model is stored inside the prob_input property of the test function instance. Print it to the terminal to see the full specification:

print(my_testfun.prob_input)

Name         : Borehole-Harper-1983
Spatial Dim. : 8
Description  : Probabilistic input model of the Borehole model from Harper and Gupta (1983).
Marginals    :

  No.   Name    Distribution        Parameters                          Description
-----  ------  --------------  ---------------------  -----------------------------------------------
    1    rw        normal      [0.1       0.0161812]            radius of the borehole [m]
    2    r       lognormal        [7.71   1.0056]                 radius of influence [m]
    3    Tu       uniform        [ 63070. 115600.]      transmissivity of upper aquifer [m^2/year]
    4    Hu       uniform          [ 990. 1100.]         potentiometric head of upper aquifer [m]
    5    Tl       uniform          [ 63.1 116. ]        transmissivity of lower aquifer [m^2/year]
    6    Hl       uniform           [700. 820.]          potentiometric head of lower aquifer [m]
    7    L        uniform          [1120. 1680.]                length of the borehole [m]
    8    Kw       uniform         [ 9985. 12045.]     hydraulic conductivity of the borehole [m/year]

Copulas      : None

Note

Copulas models the statistical dependence structure between the component (univariate) marginals. If the marginals are independent, then the copulas value is None. Currently, UQTestFuns does not support dependent probability inputs.

From the underlying probabilistic input model, a set of input values can be randomly generated. This is often useful for verification and validation purposes. For instance, to generate \(10'000\) sample points:

xx_sample = my_testfun.prob_input.get_sample(10000)
yy_sample = my_testfun(xx_sample)

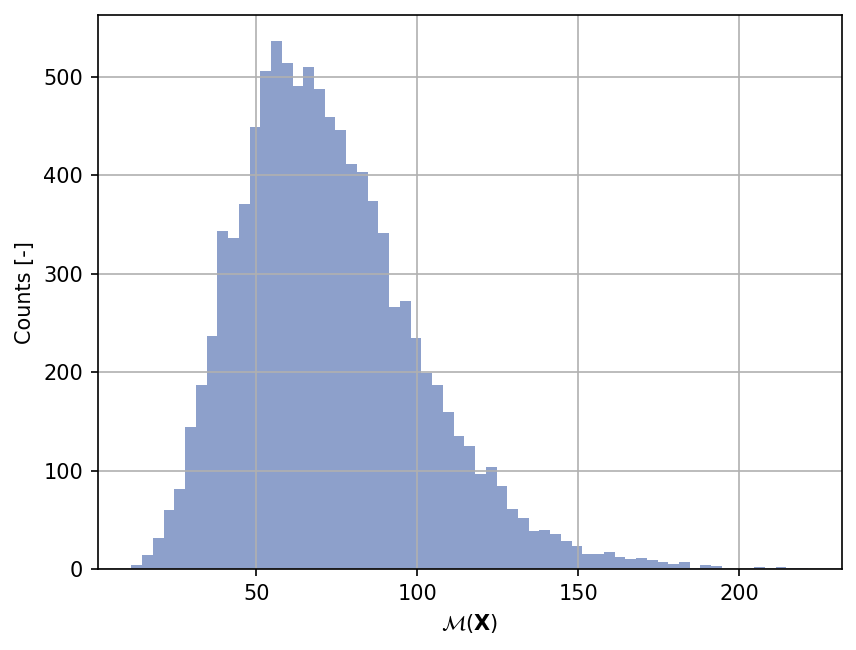
The histogram of the output values can be created as follows:

import matplotlib.pyplot as plt

plt.hist(yy_sample, bins="auto", color="#8da0cb")
plt.grid()
plt.xlabel("$\mathcal{M}(\mathbf{X})$")
plt.ylabel("Counts [-]")
plt.gcf().set_dpi(150);

../_images/tutorial-built-in-functions_15_0.png

Note

An ProbInput instance has a method called reset_rng(); You can call this method to create a new underlying RNG perhaps with a seed number. In that case, the seed number is optional; if not specified, the system entropy is used to initialized the NumPy default random generator.

In UQTestFuns, each instance of probabilistic input model carries its own pseudo-random number generator (RNG) to avoid using the global NumPy random RNG. See this blog post regarding some good practices on using NumPy RNG.

Transformation to the function domain#

Some UQ methods often produce sample points in a hypercube domain (for example, \([0, 1]^M\) or \([-1, 1]^M\) where \(M\) is the number of spatial dimension) at which the function should be evaluated. This hypercube domain may differ from the test function’s domain. Before the test function can be evaluated, those values must be first transformed to the function domain.

UQTestFuns provides a convenient function to transform sample points in one domain to the function domain. For instance, suppose we have a sample of size \(5\) in \([-1, 1]^8\) for the borehole function:

rng_1 = np.random.default_rng(42)
xx_sample_dom_1 = rng_1.uniform(low=-1, high=1, size=(5, 8))
xx_sample_dom_1

array([[ 0.5479121 , -0.12224312,  0.71719584,  0.39473606, -0.8116453 ,
         0.9512447 ,  0.5222794 ,  0.57212861],
       [-0.74377273, -0.09922812, -0.25840395,  0.85352998,  0.28773024,
         0.64552323, -0.1131716 , -0.54552256],
       [ 0.10916957, -0.87236549,  0.65526234,  0.2633288 ,  0.51617548,
        -0.29094806,  0.94139605,  0.78624224],
       [ 0.55676699, -0.61072258, -0.06655799, -0.91239247, -0.69142102,
         0.36609791,  0.48952431,  0.93501946],
       [-0.34834928, -0.25908059, -0.06088838, -0.62105728, -0.74015699,
        -0.04859015, -0.5461813 ,  0.33962799]])

We can transform this set of values to the domain of the function via the transform_sample() method:

xx_sample_trans_1 = my_testfun.transform_sample(xx_sample_dom_1)
xx_sample_trans_1

array([[1.12167271e-01, 1.91089168e+03, 1.08172149e+05, 1.06671048e+03,
        6.80819817e+01, 8.17074682e+02, 1.54623823e+03, 1.16042925e+04],
       [8.16286191e-02, 1.96768976e+03, 8.25480202e+04, 1.09194415e+03,
        9.71604649e+01, 7.98731394e+02, 1.36831195e+03, 1.04531118e+04],
       [1.02220926e-01, 4.82013357e+02, 1.06545465e+05, 1.05948308e+03,
        1.03202841e+02, 7.42543116e+02, 1.66359089e+03, 1.18248295e+04],
       [1.12406858e-01, 9.38469433e+02, 8.75868543e+04, 9.94818414e+02,
        7.12619141e+01, 7.81965874e+02, 1.53706681e+03, 1.19780700e+04],
       [9.26946708e-02, 1.59960562e+03, 8.77357668e+04, 1.01084185e+03,
        6.99728476e+01, 7.57084591e+02, 1.24706924e+03, 1.13648168e+04]])

By default, the method assumes the uniform domain of the passed values is in \([-1, 1]^M\). It is possible to transform values defined in another uniform domain. For example, the sample values in \([0, 1]^8\) (a unit hypercube):

rng_2 = np.random.default_rng(42)
xx_sample_dom_2 = rng_2.random((5, 8))
xx_sample_dom_2

array([[0.77395605, 0.43887844, 0.85859792, 0.69736803, 0.09417735,
        0.97562235, 0.7611397 , 0.78606431],
       [0.12811363, 0.45038594, 0.37079802, 0.92676499, 0.64386512,
        0.82276161, 0.4434142 , 0.22723872],
       [0.55458479, 0.06381726, 0.82763117, 0.6316644 , 0.75808774,
        0.35452597, 0.97069802, 0.89312112],
       [0.7783835 , 0.19463871, 0.466721  , 0.04380377, 0.15428949,
        0.68304895, 0.74476216, 0.96750973],
       [0.32582536, 0.37045971, 0.46955581, 0.18947136, 0.12992151,
        0.47570493, 0.22690935, 0.66981399]])

can be transformed to the domain of the borehole function as follows:

xx_sample_trans_2 = my_testfun.transform_sample(
    xx_sample_dom_2, min_value=0.0, max_value=1.0
)
xx_sample_trans_2

array([[1.12167271e-01, 1.91089168e+03, 1.08172149e+05, 1.06671048e+03,
        6.80819817e+01, 8.17074682e+02, 1.54623823e+03, 1.16042925e+04],
       [8.16286191e-02, 1.96768976e+03, 8.25480202e+04, 1.09194415e+03,
        9.71604649e+01, 7.98731394e+02, 1.36831195e+03, 1.04531118e+04],
       [1.02220926e-01, 4.82013357e+02, 1.06545465e+05, 1.05948308e+03,
        1.03202841e+02, 7.42543116e+02, 1.66359089e+03, 1.18248295e+04],
       [1.12406858e-01, 9.38469433e+02, 8.75868543e+04, 9.94818414e+02,
        7.12619141e+01, 7.81965874e+02, 1.53706681e+03, 1.19780700e+04],
       [9.26946708e-02, 1.59960562e+03, 8.77357668e+04, 1.01084185e+03,
        6.99728476e+01, 7.57084591e+02, 1.24706924e+03, 1.13648168e+04]])

Note that for a given sample, the bounds of the hypercube domain must be the same in all dimensions.

The two transformed values above should be the same since we use two instances of the default RNG with the same seed to generate the random sample.

assert np.allclose(xx_sample_trans_1, xx_sample_trans_2)
assert np.allclose(my_testfun(xx_sample_trans_1), my_testfun(xx_sample_trans_2))

Test functions with parameters#

Some test functions are parameterized; this means that to fully specify the function, an additional set of values must be specified. In principle, these parameter values can be anything: numerical values, flags, selection using strings, etc.

For instance, consider the Ishigami function [IH91] defined as follows:

\[ \mathcal{M}(\boldsymbol{x}) = \sin{(x_1)} + a \sin^2{(x_2)} + b x_3^4 \sin{(x_1)} \]

where \(a\) and \(b\) are the so-called parameters of the function. Before the function can be evaluated, these parameters must be assigned to some values. The default Ishigami function in UQTestFuns has these values given and stored in the parameters property:

my_testfun = uqtf.Ishigami()
my_testfun.parameters

(7, 0.05)

To assign different parameter values, override the property values of the instance. For example:

my_testfun.parameters = (7, 0.35)
my_testfun.parameters

(7, 0.35)

Note that once set, the parameter values are kept constant during the evaluation of the function on a set of input values

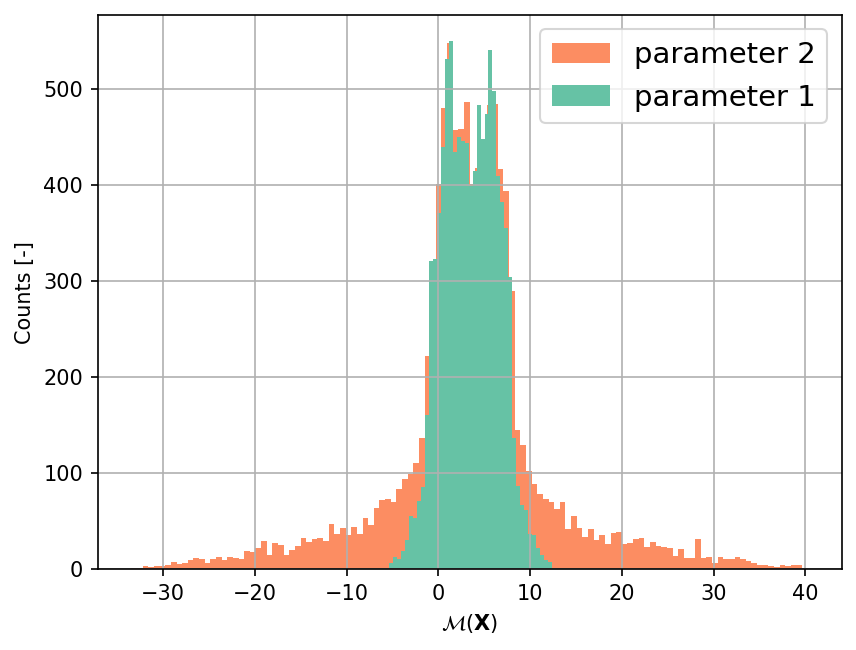
Different parameter values usually change the overall behavior of the function. In the case of the Ishigami function, different parameter values alter the total variance of the output as illustrated in the figure below.

../_images/tutorial-built-in-functions_31_0.png

Test functions with variable dimension#

Some test functions support a variable dimension, meaning that an instance of a test function can be constructed for any number (positive integer, please) of spatial dimension.

Consider, for instance, the Sobol’-G function [SSobol95], a test function whose dimension can be varied and a popular choice in the context of sensitivity analysis. It is defined as follows:

\[ \mathcal{M}(\boldsymbol{x}) = \prod_{m = 1}^M \frac{\lvert 4 x_m - 2 \rvert + a_m}{1 + a_m} \]

where \(\boldsymbol{x} = \{ x_1, \ldots, x_M \}\) is the \(M\)-dimensional vector of input variables, and \(\boldsymbol{a} = \{ a_1, \ldots, a_M \}\) are parameters of the function.

To create a six-dimensional Sobol’-G function, use the parameter spatial_dimension to specify the desired dimensionality:

my_testfun = uqtf.SobolG(spatial_dimension=6)

Verify that the function is indeed a six-dimension one:

print(my_testfun)

Name              : SobolG
Spatial dimension : 6
Description       : Sobol'-G function from Saltelli and Sobol' (1995)

and:

print(my_testfun.prob_input)

Name         : Sobol-G-Saltelli1995
Spatial Dim. : 6
Description  : Probabilistic input model for the Sobol'-G function from Saltelli and Sobol' (1995)
Marginals    :

  No.   Name    Distribution    Parameters    Description
-----  ------  --------------  ------------  -------------
    1    X1       uniform        [0. 1.]         None
    2    X2       uniform        [0. 1.]         None
    3    X3       uniform        [0. 1.]         None
    4    X4       uniform        [0. 1.]         None
    5    X5       uniform        [0. 1.]         None
    6    X6       uniform        [0. 1.]         None

Copulas      : None

References#

HG83: William V. Harper and Sumant K. Gupta. Sensitivity/uncertainty analysis of a borehole scenario comparing latin hypercube sampling and deterministic sensitivity approaches. Technical Report BMI/ONWI-516, Office of Nuclear Waste Isolation, Battelle Memorial Institute, 1983. URL: https://inldigitallibrary.inl.gov/PRR/84393.pdf.
IH91: T. Ishigami and T. Homma. An importance quantification technique in uncertainty analysis for computer models. In [1990] Proceedings. First International Symposium on Uncertainty Modeling and Analysis, 398–403. IEEE Comput. Soc. Press, 1991. doi:10.1109/ISUMA.1990.151285.
SSobol95: Andrea Saltelli and Ilya M. Sobol'. About the use of rank transformation in sensitivity analysis of model output. Reliability Engineering & System Safety, 50(3):225–239, 1995. doi:10.1016/0951-8320(95)00099-2.

UQTestFuns

Tutorial: Create Built-in Test Functions

Contents

Tutorial: Create Built-in Test Functions#

Listing available test functions#

A Callable instance#

Probabilistic input#

Transformation to the function domain#

Test functions with parameters#

Test functions with variable dimension#

References#