Gayton Hat Function#

import numpy as np
import matplotlib.pyplot as plt
import uqtestfuns as uqtf

The Gayton Hat function is a two-dimensional function used in [EGLR13] as a test function for reliability analysis algorithms.

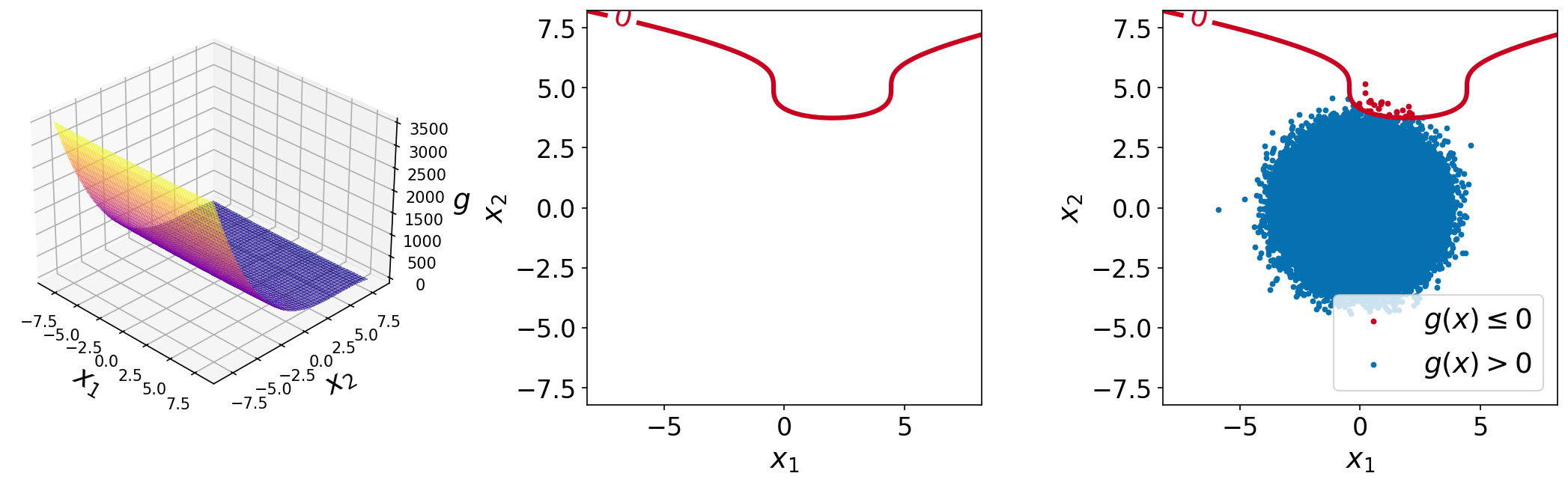
The plots of the function are shown below. The left plot shows the surface plot of the performance function, the center plot shows the contour plot with a single contour line at function value of \(0.0\) (the limit-state surface), and the right plot shows the same plot with \(10^6\) sample points overlaid.

../_images/gayton-hat_3_0.png

Test function instance#

To create a default instance of the test function:

my_testfun = uqtf.GaytonHat()

Check if it has been correctly instantiated:

print(my_testfun)

Name              : GaytonHat
Spatial dimension : 2
Description       : Two-Dimensional Gayton Hat function from Echard et al. (2013)

Description#

The test function (i.e., the performance function) is analytically defined as follows:

\[ g(\boldsymbol{x}) = 0.5 (u_1 - 2)^2 - 1.5 (u_2 - 5)^3 - 3, \]

where \(\boldsymbol{x} = \{ u_1, u_2 \}\) is the two-dimensional vector of input variables probabilistically defined further below.

The failure state and the failure probability are defined as \(g(\boldsymbol{x}) \leq 0\) and \(\mathbb{P}[g(\boldsymbol{X}) \leq 0]\), respectively.

Probabilistic input#

Based on [EGLR13], the probabilistic input model for the test function consists of two independent standard normal random variables (see the table below).

my_testfun.prob_input

Name: Echard2013

Spatial Dimension: 2

Description: Input model for the Gayton Hat function from Echard et al. (2013)

Marginals:

No. Name Distribution Parameters Description
1 U1 normal [0 1] None
2 U2 normal [0 1] None

Copulas: None

Reference results#

This section provides several reference results of typical UQ analyses involving the test function.

Sample histogram#

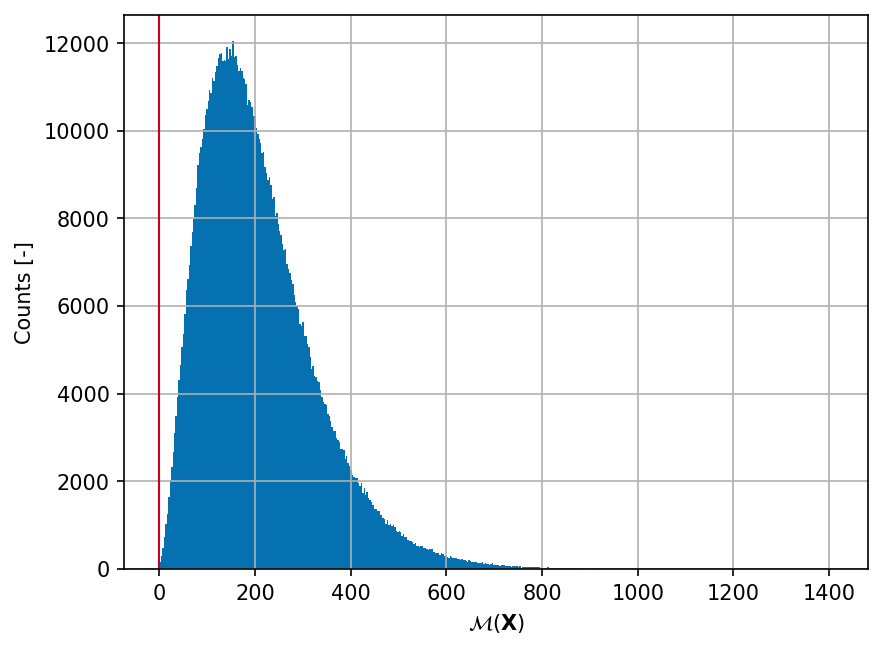
Shown below is the histogram of the output based on \(10^6\) random points:

xx_test = my_testfun.prob_input.get_sample(1000000)
yy_test = my_testfun(xx_test)
idx_pos = yy_test > 0
idx_neg = yy_test <= 0

hist_pos = plt.hist(yy_test, bins="auto", color="#0571b0")
plt.hist(yy_test[idx_neg], bins=hist_pos[1], color="#ca0020")
plt.axvline(0, linewidth=1.0, color="#ca0020")

plt.grid()
plt.ylabel("Counts [-]")
plt.xlabel("$\mathcal{M}(\mathbf{X})$")
plt.gcf().set_dpi(150);
../_images/gayton-hat_11_0.png

Failure probability (\(P_f\))#

Some reference values for the failure probability \(P_f\) from the literature are summarized in the table below.

Method

\(N\)

\(\hat{P}_f\)

\(\mathrm{CoV}[\hat{P}_f]\)

Source

Remark

MCS

\(5 \times 10^7\)

\(2.85 \times 10^{-5}\)

\(2.64 \%\)

[EGLR13]

Median over \(100\) replications

FORM

\(19\)

\(4.21 \times 10^{-5}\)

—

[EGLR13]

Median over \(100\) replications

IS

\(19 + \times 10^4\)

\(2.86 \times 10^{-5}\)

\(2.39 \%\)

[EGLR13]

Median over \(100\) replications

AK+IS1

\(19 + 7\)

\(2.86 \times 10^{-5}\)

\(2.39 \%\)

[EGLR13]

Median over \(100\) replications

References#

EGLR13(1,2,3,4,5,6)

B. Echard, N. Gayton, M. Lemaire, and N. Relun. A combined importance sampling and kriging reliability method for small failure probabilities with time-demanding numerical models. Reliability Engineering & System Safety, 111:232–240, 2013. doi:10.1016/j.ress.2012.10.008.

1

Adaptive-Kriging importance sampling