Piston Simulation Function#

import numpy as np
import matplotlib.pyplot as plt
import uqtestfuns as uqtf

The Piston simulation test function is a seven-dimensional scalar-valued function. The function computes the cycle time of a piston system.

This function has been used as a test function in metamodeling exercises [BAS07]. A 20-dimensional variant was used in the context of sensitivity analysis [Moo10] by introducing 13 additional inert input variables.

Test function instance#

To create a default instance of the piston simulation test function:

my_testfun = uqtf.Piston()

Check if it has been correctly instantiated:

print(my_testfun)

Name              : Piston
Spatial dimension : 7
Description       : Piston simulation model from Ben-Ari and Steinberg (2007)

Description#

The Piston simulation computes the cycle time of a piston moving inside a cylinder using the following analytical expression:

\[\begin{split} \begin{align} \mathcal{M}(\boldsymbol{x}) & = 2 \pi \left( \frac{M}{k + S^2 \frac{P_0 V_0}{T_0} \frac{T_a}{V^2}} \right)^{0.5}, \\ V & = \frac{S}{2 k} \left[ \left(A^2 + 4 k \frac{P_0 V_0}{T_0} T_a \right)^{0.5} - A \right]^{0.5}, \\ A & = P_0 S + 19.62 M - \frac{k V_0}{S}, \end{align} \end{split}\]

where \(\boldsymbol{x} = \{ M, S, V_0, k, P_0, T_a, T_0 \}\) is the seven-dimensional vector of input variables further defined below.

Probabilistic input#

Two probabilistic input model specifications for the OTL circuit function are available as shown in the table below.

No.

Keyword

Source

1.

BenAri2007 (default)

[BAS07]

2.

Moon2010

[Moo10]

The default selection, based on [BAS07], contains seven input variables given as independent uniform random variables with specified ranges shown in the table below.

my_testfun.prob_input

Name: Piston-BenAri2007

Spatial Dimension: 7

Description: Probabilistic input model for the Piston simulation model from Ben-Ari and Steinberg (2007).

Marginals:

No. Name Distribution Parameters Description
1 M uniform [30. 60.] Piston weight [kg]
2 S uniform [0.005 0.02 ] Piston surface area [m^2]
3 V0 uniform [0.002 0.01 ] Initial gas volume [m^3]
4 k uniform [1000. 5000.] Spring coefficient [N/m]
5 P0 uniform [ 90000. 110000.]Atmospheric pressure [N/m^2]
6 Ta uniform [290. 296.] Ambient temperature [K]
7 T0 uniform [340. 360.] Filling gas temperature [K]

Copulas: None

Note

In [Moo10], 13 additional inert independent input variables are introduced (totaling 20 input variables); these input variables, being inert, do not affect the output of the function.

To create an instance of the piston simulation test function with the probabilistic input specified in [Moo10], pass the corresponding keyword ("Moon2010") to the parameter (prob_input_selection):

my_testfun = uqtf.Piston(prob_input_selection="Moon2010")

Reference results#

This section provides several reference results of typical UQ analyses involving the test function.

Sample histogram#

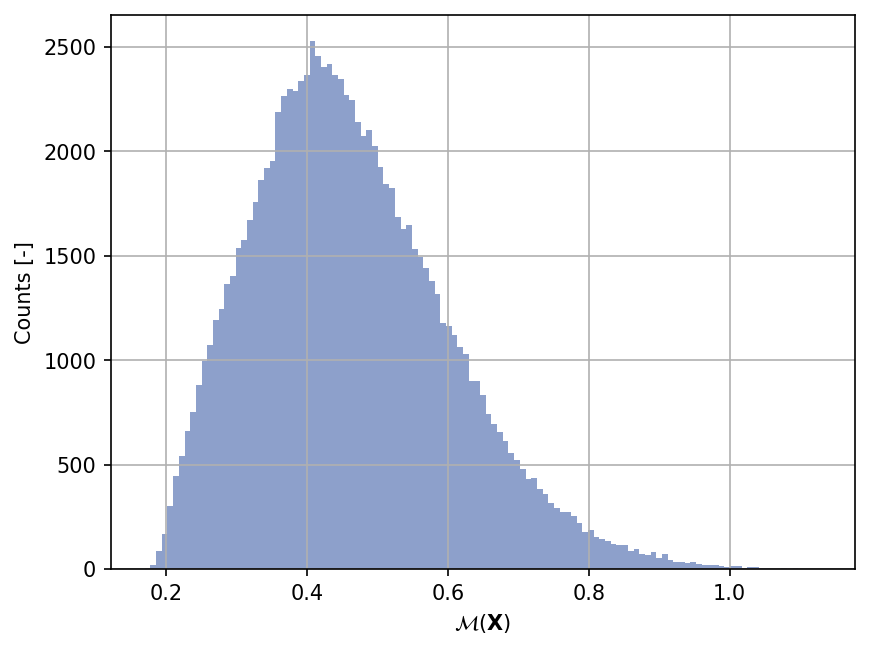
Shown below is the histogram of the output based on \(100'000\) random points:

np.random.seed(42)
xx_test = my_testfun.prob_input.get_sample(100000)
yy_test = my_testfun(xx_test)

plt.hist(yy_test, bins="auto", color="#8da0cb");
plt.grid();
plt.ylabel("Counts [-]");
plt.xlabel("$\mathcal{M}(\mathbf{X})$");
plt.gcf().set_dpi(150);
../_images/piston_9_0.png

Moments estimation#

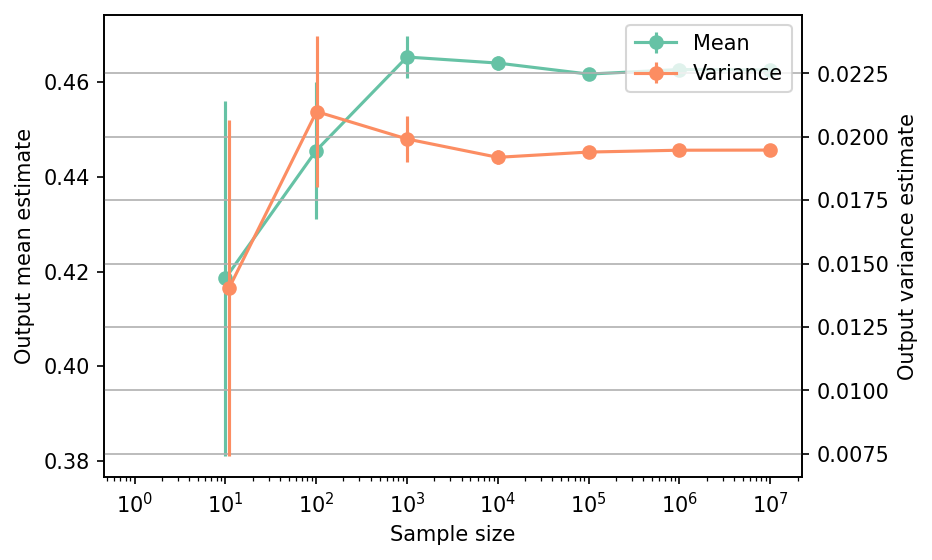
Shown below is the convergence of a direct Monte-Carlo estimation of the output mean and variance with increasing sample sizes.

# --- Compute the mean and variance estimate
np.random.seed(42)
sample_sizes = np.array([1e1, 1e2, 1e3, 1e4, 1e5, 1e6, 1e7], dtype=int)
mean_estimates = np.empty(len(sample_sizes))
var_estimates = np.empty(len(sample_sizes))

for i, sample_size in enumerate(sample_sizes):
    xx_test = my_testfun.prob_input.get_sample(sample_size)
    yy_test = my_testfun(xx_test)
    mean_estimates[i] = np.mean(yy_test)
    var_estimates[i] = np.var(yy_test)

# --- Compute the error associated with the estimates
mean_estimates_errors = np.sqrt(var_estimates) / np.sqrt(np.array(sample_sizes))
var_estimates_errors = var_estimates * np.sqrt(2 / (np.array(sample_sizes) - 1))

# --- Do the plot
fig, ax_1 = plt.subplots(figsize=(6,4))

ax_1.errorbar(
    sample_sizes,
    mean_estimates,
    yerr=mean_estimates_errors,
    marker="o",
    color="#66c2a5",
    label="Mean",
)
ax_1.set_xlabel("Sample size")
ax_1.set_ylabel("Output mean estimate")
ax_1.set_xscale("log");
ax_2 = ax_1.twinx()
ax_2.errorbar(
    sample_sizes + 1,
    var_estimates,
    yerr=var_estimates_errors,
    marker="o",
    color="#fc8d62",
    label="Variance",
)
ax_2.set_ylabel("Output variance estimate")

# Add the two plots together to have a common legend
ln_1, labels_1 = ax_1.get_legend_handles_labels()
ln_2, labels_2 = ax_2.get_legend_handles_labels()
ax_2.legend(ln_1 + ln_2, labels_1 + labels_2, loc=0)

plt.grid()
fig.set_dpi(150)
../_images/piston_11_0.png

The tabulated results for each sample size is shown below.

from tabulate import tabulate

# --- Compile data row-wise
outputs = []
for (
    sample_size,
    mean_estimate,
    mean_estimate_error,
    var_estimate,
    var_estimate_error,
) in zip(
    sample_sizes,
    mean_estimates,
    mean_estimates_errors,
    var_estimates,
    var_estimates_errors,
):
    outputs += [
        [
            sample_size,
            mean_estimate,
            mean_estimate_error,
            var_estimate,
            var_estimate_error,
            "Monte-Carlo",
        ],
    ]

header_names = [
    "Sample size",
    "Mean",
    "Mean error",
    "Variance",
    "Variance error",
    "Remark",
]

tabulate(
    outputs,
    headers=header_names,
    floatfmt=(".1e", ".4e", ".4e", ".4e", ".4e", "s"),
    tablefmt="html",
    stralign="center",
    numalign="center",
)
Sample size Mean Mean error Variance Variance error Remark
1.0e+01 4.1856e-01 3.7467e-02 1.4038e-02 6.6174e-03 Monte-Carlo
1.0e+02 4.4553e-01 1.4489e-02 2.0994e-02 2.9840e-03 Monte-Carlo
1.0e+03 4.6529e-01 4.4625e-03 1.9914e-02 8.9102e-04 Monte-Carlo
1.0e+04 4.6402e-01 1.3853e-03 1.9191e-02 2.7141e-04 Monte-Carlo
1.0e+05 4.6169e-01 4.4044e-04 1.9398e-02 8.6753e-05 Monte-Carlo
1.0e+06 4.6265e-01 1.3954e-04 1.9471e-02 2.7536e-05 Monte-Carlo
1.0e+07 4.6257e-01 4.4132e-05 1.9476e-02 8.7100e-06 Monte-Carlo

References#

BAS07(1,2,3)

Einat Neumann Ben-Ari and David M. Steinberg. Modeling data from computer experiments: an empirical comparison of kriging with MARS and projection pursuit regression. Quality Engineering, 19(4):327–338, 2007. doi:10.1080/08982110701580930.

Moo10(1,2,3,4)

Hyejung Moon. Design and analysis of computer experiments for screening input variables. PhD thesis, Ohio State University, Ohio, 2010. URL: http://rave.ohiolink.edu/etdc/view?acc_num=osu1275422248.