Damped Oscillator Reliability#

import numpy as np
import matplotlib.pyplot as plt
import uqtestfuns as uqtf

The damped oscillator reliability problem is an eight-dimensional reliability analysis test function [DKDS91, Dub11, DKDS90, BDL11].

Note

The reliability analysis variant differs from the base model. The base model computes the mean-square relative displacement of the secondary spring without reference to the performance of the system.

Test function instance#

To create a default instance of the test function:

my_testfun = uqtf.DampedOscillatorReliability()

Check if it has been correctly instantiated:

print(my_testfun)

Name              : DampedOscillatorReliability
Spatial dimension : 8
Description       : Performance function from Der Kiureghian and De Stefano (1990)

Description#

The problem poses the reliability of a damped oscillator system as defined in [IK85] (see Damped Oscillator). The reliability of the system depends on the secondary spring as described by the following performance function [Dub11, DKDS90] 1:

\[ g(\boldsymbol{x}; p) = F_s - p k_s \mathcal{M}(M_p, M_s, K_p, K_s, \zeta_p, \zeta_s, S_0), \]
\[ \mathcal{M}(M_p, M_s, K_p, K_s, \zeta_p, \zeta_s, S_0) = \left( \pi \frac{S_0}{4 \zeta_s \omega_s^3} \frac{\zeta_a \zeta_s}{\zeta_p \zeta_s (4 \zeta_a^2 + \theta^2) + \gamma \zeta_a^2} \frac{(\zeta_p \omega_p^3 + \zeta_s \omega_s^3) \omega_p}{4 \zeta_a \omega_a^4} \right)^{0.5} \]
\[\begin{split} \begin{aligned} \omega_p & = \left( \frac{k_p}{m_p}\right)^{0.5} & \omega_s & = \left(\frac{k_s}{m_s}\right)^{0.5} & \omega_a & = \frac{\omega_p + \omega_s}{2}\\ \gamma & = \frac{m_s}{m_p} & \zeta_a & = \frac{\zeta_p + \zeta_s}{2} & \theta & = \frac{\omega_p - \omega_s}{\omega_a} \\ \end{aligned} \end{split}\]

where \(\boldsymbol{x} = \{ M_p, M_s, K_p, K_s, \zeta_p, \zeta_s, S_0, F_s \}\) is the eight-dimensional vector of input variables probabilistically defined further below and \(p\) is a deterministic parameter of the function (i.e., the peak factor).

The failure state and the failure probability are defined as \(g(\boldsymbol{x}; p) \leq 0\) and \(\mathbb{P}[g(\boldsymbol{X}; p) \leq 0]\), respectively.

Probabilistic input#

Based on [DKDS91], the probabilistic input model for the damped oscillator reliability consists of eight independent random variables with marginal distributions shown in the table below.

my_testfun.prob_input

Name: DampedOscillatorReliability-DerKiureghian1990a

Spatial Dimension: 8

Description: Input model #1 for the damped oscillator reliability from Der Kiureghian and De Stefano (1990)

Marginals:

No. Name Distribution Parameters Description
1 Mp lognormal [0.40048994 0.09975135] Primary mass
2 Ms lognormal [-4.61014535 0.09975135] Secondary mass
3 Kp lognormal [-0.01961036 0.1980422 ] Primary spring stiffness
4 Ks lognormal [-4.62478054 0.1980422 ] Secondary spring stiffness
5Zeta_p lognormal [-3.06994228 0.38525317] Primary damping ratio
6Zeta_s lognormal [-4.02359478 0.47238073] Secondary damping ratio
7 S0 lognormal [4.60019502 0.09975135] White noise base acceleration
8 Fs lognormal [2.70307504 0.09975135] Force capacity of the secondary spring

Copulas: None

In the literature, the force capacity of the secondary spring (i.e., \(F_s\)) have different probabilistic specifications as summarized in the table below.

\(F_S\)

Keyword

Source

\(\mathcal{N}_{\mathrm{log}}(15.0, 1.50)\)

DerKiureghian1990a (default)

[DKDS90]

\(\mathcal{N}_{\mathrm{log}}(21.5, 2.15)\)

DerKiureghian1990b

[DKDS90]

\(\mathcal{N}_{\mathrm{log}}(27.5, 2.75)\)

DerKiureghian1990c

[DKDS90]

Note that the parameters of the log-normal distribution given above correspond to the mean and standard deviation of the log-normal distribution (and not the mean and standard deviation of the underlying normal distribution).

With the higher mean of \(F_s\), the failure probability becomes smaller.

Parameters#

The performance function contains a single parameter (peak factor). From [DKDS91] this parameter is set to \(3\).

Reference results#

This section provides several reference results of typical UQ analyses involving the test function.

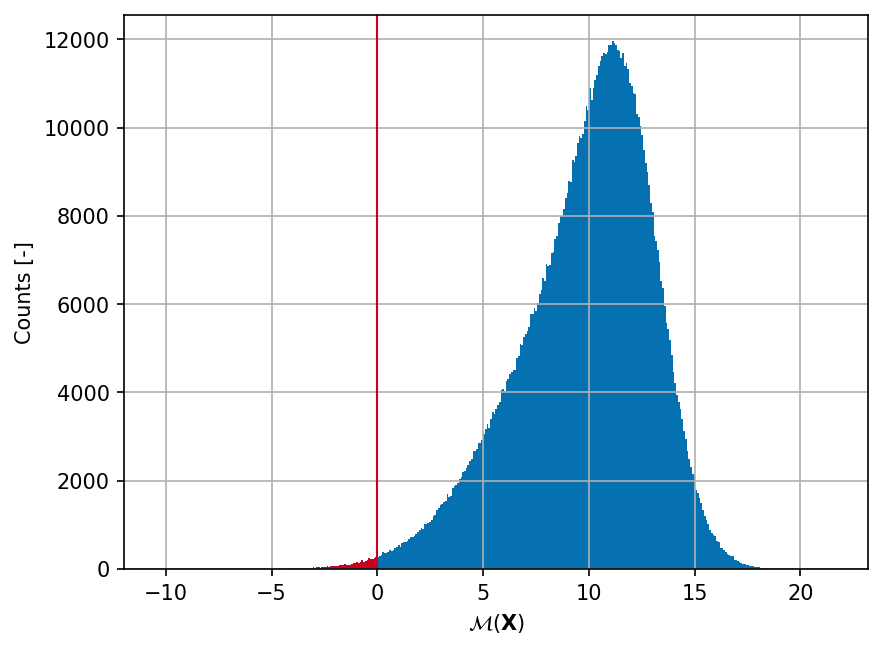
Sample histogram#

Shown below is the histogram of the output based on \(10^6\) random points:

xx_test = my_testfun.prob_input.get_sample(1000000)
yy_test = my_testfun(xx_test)
idx_pos = yy_test > 0
idx_neg = yy_test <= 0

hist_pos = plt.hist(yy_test, bins="auto", color="#0571b0")
plt.hist(yy_test[idx_neg], bins=hist_pos[1], color="#ca0020")
plt.axvline(0, linewidth=1.0, color="#ca0020")

plt.grid()
plt.ylabel("Counts [-]")
plt.xlabel("$\mathcal{M}(\mathbf{X})$")
plt.gcf().set_dpi(150);
../_images/damped-oscillator-reliability_9_0.png

Failure probability#

Some reference values for the failure probability \(P_f\) and from the literature are summarized in the table below (\(\mu_{F_s}\) is the log-normal distribution mean of \(F_s\)).

\(\mu_{F_s}\)

Method

\(N\)

\(\hat{P}_f\)

\(\mathrm{CoV}[\hat{P}_f]\)

Source

\(15\)

FORM

\(1'179\)

\(2.19 \times 10^{-2}\)

—

[DKDS90, BDL11]

SS

\(3 \times 10^5\)

\(4.63 \times 10^{-3}\)

\(< 3\%\)

[Dub11]

Meta-IS2

\(464 + 600\)

\(4.80 \times 10^{-3}\)

\(< 5\%\)

[Dub11]

SVM + SS

\(1'719\)

\(4.78 \times 10^{-3}\)

\(< 4\%\)

[BDL11]

\(21.5\)

FORM

\(2'520\)

\(3.50 \times 10^{-4}\)

—

[DKDS90, BDL11]

SS

\(5 \times 10^5\)

\(4.75 \times 10^{-5}\)

\(< 4\%\)

[Dub11]

Meta-IS

\(336 + 400\)

\(4.46 \times 10^{-5}\)

\(< 5\%\)

[Dub11]

SVM + SS

\(2'865\)

\(4.42 \times 10^{-5}\)

\(< 7\%\)

[BDL11]

\(27.5\)

FORM

\(2'727\)

\(3.91 \times 10^{-6}\)

—

[DKDS90, BDL11]

SS

\(7 \times 10^5\)

\(3.47 \times 10^{-7}\)

\(< 5\%\)

[Dub11]

Meta-IS

\(480 + 200\)

\(3.76 \times 10^{-7}\)

\(< 5\%\)

[Dub11]

SVM + SS

\(4'011\)

\(3.66 \times 10^{-7}\)

\(< 10\%\)

[BDL11]

Note that in the table above the total number of model evaluations for metamodel-based Importance Sampling (Meta-IS) is the sum of training runs and the correction runs [Dub11].

References#

IK85

Takeru Igusa and Armen Der Kiureghian. Dynamic characterization of two-degree-of-freedom equipment-structure systems. Journal of Engineering Mechanics, 111(1):1–19, 1985. doi:10.1061/(asce)0733-9399(1985)111:1(1).

DKDS91(1,2,3)

Armen Der Kiureghian and Mario De Stefano. Efficient algorithm for second-order reliability analysis. Journal of Engineering Mechanics, 117(12):2904–2923, 1991. doi:10.1061/(asce)0733-9399(1991)117:12(2904).

Dub11(1,2,3,4,5,6,7,8,9,10)

Vincent Dubourg. Adaptive surrogate models for reliability analysis and reliability-based design optimization. phdthesis, Université Blaise Pascal - Clermont II, Clermont-Ferrand, France, 2011.

DKDS90(1,2,3,4,5,6,7,8)

Armen Der Kiureghian and Mario De Stefano. An efficient algorithm for second-order reliability analysis. techreport UCB/SEMM-90/20, Department of Civil and Environmental Engineering, University of California, Berkeley, 1990.

BDL11(1,2,3,4,5,6,7)

J.-M. Bourinet, F. Deheeger, and M. Lemaire. Assessing small failure probabilities by combined subset simulation and support vector machines. Structural Safety, 33(6):343–353, 2011. doi:10.1016/j.strusafe.2011.06.001.

1

see, for instance, Eqs. (5.5) and (5.7), pp. 184-185 in [Dub11].

2

Metamodel-based Importance Sampling