Welch et al. (1992) Function#

import numpy as np
import matplotlib.pyplot as plt
import uqtestfuns as uqtf

The Welch et al. (1992) test function (or the Welch1992 function for short) is a 20-dimensional scalar-valued function. The function features some strong non-linearities as well as some pair interaction effects. Furthermore, a couple of two input variables are set to be inert.

The function was introduced in Welch et al. (1992) [WBS+92] as a test function for metamodeling and sensitivity analysis purposes. The function is also suitable for testing multi-dimensional integration algorithms.

Test function instance#

To create a default instance of the test function:

my_testfun = uqtf.Welch1992()

Check if it has been correctly instantiated:

print(my_testfun)

Name              : Welch1992
Spatial dimension : 20
Description       : 20-Dimensional function from Welch et al. (1992)

Description#

The Welch1992 function is defined as follows1:

\[\begin{split} \begin{aligned} \mathcal{M}(\boldsymbol{x}) = & \frac{5 x_{12}}{1 + x_1} + 5 (x_4 - x_{20})^2 + x_5 + 40 x_{19}^3 - 5 x_{19} \\ & + 0.05 x_2 + 0.08 x_3 - 0.03 x_6 + 0.03 x_7 \\ & - 0.09 x_9 - 0.01 x_{10} - 0.07 x_{11} + 0.25 x_{13}^2 \\ & - 0.04 x_{14} + 0.06 x_{15} - 0.01 x_{17} - 0.03 x_{18}, \end{aligned} \end{split}\]

where \(\boldsymbol{x} = \{ x_1, \ldots, x_{20} \}\) is the 20-dimensional vector of input variables further defined below. Notice that the input variables \(x_8\) and \(x_{16}\) are inert and therefore, missing from the expression.

Probabilistic input#

Based on [WBS+92], the test function is defined on the 20-dimensional input space \([-0.5, 0.5]^{20}\). This input can be modeled using 20 independent uniform random variables shown in the table below.

my_testfun.prob_input

Name: Welch1992

Spatial Dimension: 20

Description: Input specification for the test function from Welch et al. (1992)

Marginals:

No. Name Distribution Parameters Description
1 x1 uniform [-0.5 0.5] None
2 x2 uniform [-0.5 0.5] None
3 x3 uniform [-0.5 0.5] None
4 x4 uniform [-0.5 0.5] None
5 x5 uniform [-0.5 0.5] None
6 x6 uniform [-0.5 0.5] None
7 x7 uniform [-0.5 0.5] None
8 x8 uniform [-0.5 0.5] None
9 x9 uniform [-0.5 0.5] None
10 x10 uniform [-0.5 0.5] None
11 x11 uniform [-0.5 0.5] None
12 x12 uniform [-0.5 0.5] None
13 x13 uniform [-0.5 0.5] None
14 x14 uniform [-0.5 0.5] None
15 x15 uniform [-0.5 0.5] None
16 x16 uniform [-0.5 0.5] None
17 x17 uniform [-0.5 0.5] None
18 x18 uniform [-0.5 0.5] None
19 x19 uniform [-0.5 0.5] None
20 x20 uniform [-0.5 0.5] None

Copulas: None

Reference Results#

This section provides several reference results of typical analyses involving the test function.

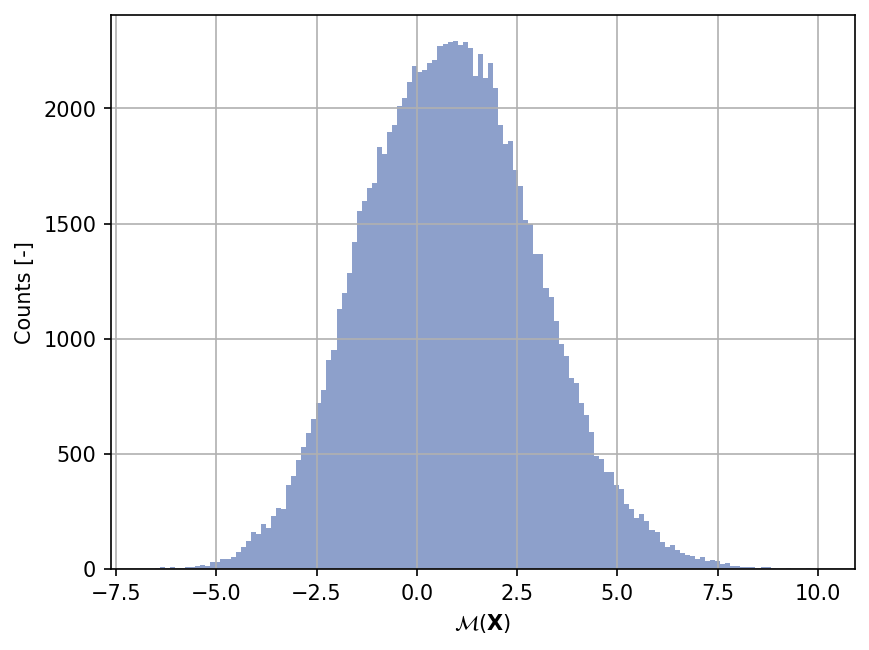
Sample histogram#

Shown below is the histogram of the output based on \(100'000\) random points:

np.random.seed(42)
xx_test = my_testfun.prob_input.get_sample(100000)
yy_test = my_testfun(xx_test)

plt.hist(yy_test, bins="auto", color="#8da0cb");
plt.grid();
plt.ylabel("Counts [-]");
plt.xlabel("$\mathcal{M}(\mathbf{X})$");
plt.gcf().set_dpi(150);
../_images/welch1992_9_0.png

Definite integration#

The integral value of the test function over the domain \([-0.5, 0.5]^{20}\) is analytical:

\[ I[\mathcal{M}] = \int_{[-0.5, 0.5]^{20}} \mathcal{M}(\boldsymbol{x}) \; d\boldsymbol{x} = \frac{41}{48}. \]

Moments estimation#

The moments of the test function may be derived analytically; the first two (i.e., the expected value and the variance) are given below.

Expected value#

Due to the fact that the function domain is a hypercube and the input variables are uniformly distributed, the expected value of the function is the same as the integral value over the domain:

\[ \mathbb{E}[\mathcal{M}] = \frac{41}{48}. \]

Variance#

The analytical value (albeit inexact) for the variance is given as follows:

\[ \mathbb{V}[\mathcal{M}] \approx 5.2220543. \]

References#

WBS+92(1,2,3)

William J. Welch, Robert. J. Buck, Jerome Sacks, Henry P. Wynn, Toby J. Mitchell, and Max D. Morris. Screening, predicting, and computer experiments. Technometrics, 34(1):15, 1992. doi:10.2307/1269548.

1

see Section 3.1, p. 20 in [WBS+92].