Sobol’-G Function#

The Sobol’-G function is an \(M\)-dimensional scalar-valued function. It was introduced in [RSobolT96] for testing numerical integration algorithms (e.g., quasi-Monte-Carlo; see for instance [Sobol98]. Later on, it becomes a popular testing function for global sensitivity analysis methods; see, for instances, [MILR09, MIVDV08, KFSM11].

The Sobol’-G function is an M-dimensional scalar-valued function. It was introduced in [1] for testing numerical integration algorithms (e.g., quasi-Monte-Carlo; see also for instance [2] and [3]). The current form (and name) was from [4] and used in the context of global sensitivity analysis. There, the function was generalized by introducing a set of parameters that determines the importance of each input variable. Later on, it becomes a popular testing function for global sensitivity analysis methods; see, for instances, [5], [6], and [7].

import numpy as np
import matplotlib.pyplot as plt
import uqtestfuns as uqtf

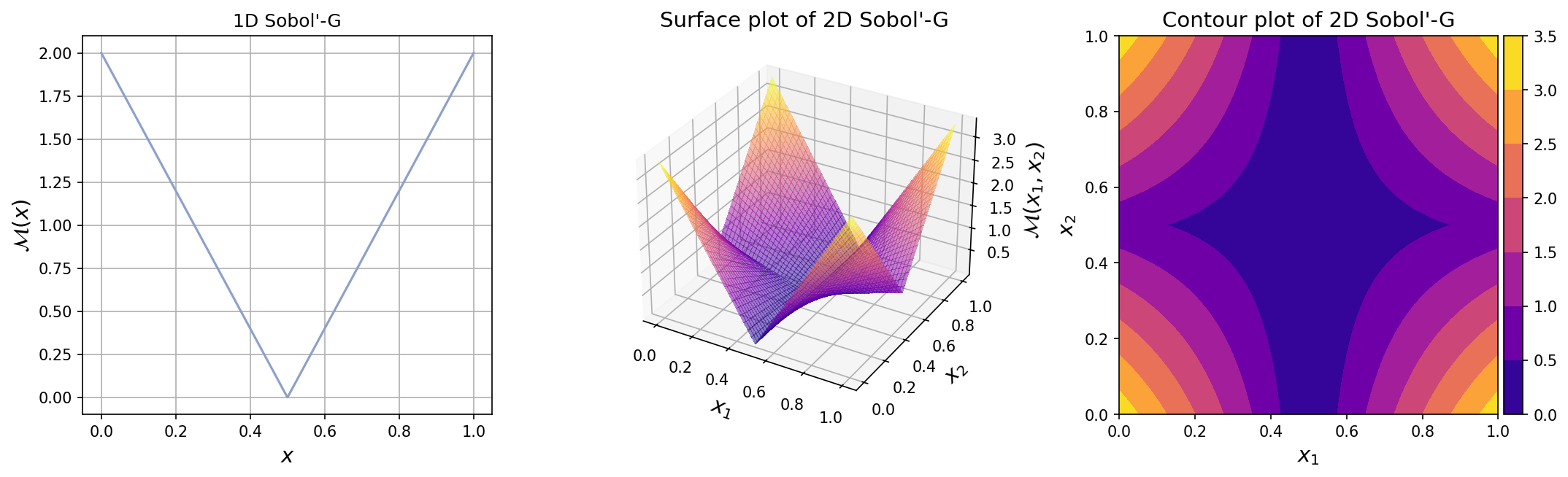
The plots for one-dimensional and two-dimensional Sobol’-G function can be seen below.

../_images/sobol-g_3_0.png

Test function instance#

To create a default instance of the Sobol’-G test function, type:

my_testfun = uqtf.SobolG()

Check if it has been correctly instantiated:

print(my_testfun)

Name              : SobolG
Spatial dimension : 2
Description       : Sobol'-G function from Saltelli and Sobol' (1995)

By default, the spatial dimension is set to \(2\)1. To create an instance with another value of spatial dimension, pass an integer to the parameter spatial_dimension (keyword only). For example, to create an instance of the Sobol’-G function in six dimensions, type:

my_testfun = uqtf.SobolG(spatial_dimension=6)

In the subsequent section, the function will be illustrated using six dimensions.

Description#

The Sobol’-G function is defined as follows2:

\[ \mathcal{M}(\boldsymbol{x}) = \prod_{m = 1}^M \frac{\lvert 4 x_m - 2 \rvert + a_m}{1 + a_m} \]

where \(\boldsymbol{x} = \{ x_1, \ldots, x_M \}\) is the \(M\)-dimensional vector of input variables further defined below, and \(\boldsymbol{a} = \{ a_1, \ldots, a_M \}\) are parameters of the function.

Probabilistic input#

Based on [Sobol98] the probabilistic input model for the Sobol’-G function consists of \(M\) independent uniform random variables with the ranges shown in the table below.

my_testfun.prob_input

Name: Sobol-G-Saltelli1995

Spatial Dimension: 6

Description: Probabilistic input model for the Sobol'-G function from Saltelli and Sobol' (1995)

Marginals:

No. Name Distribution Parameters Description
1 X1 uniform [0. 1.] None
2 X2 uniform [0. 1.] None
3 X3 uniform [0. 1.] None
4 X4 uniform [0. 1.] None
5 X5 uniform [0. 1.] None
6 X6 uniform [0. 1.] None

Copulas: None

Parameters#

The parameters of the Sobol-G function (that is, the coefficients \(\{ a_m \}\)) determine the overall behavior of the function as well as the importance of each input variable. There are several sets of parameters used in the literature as shown in the table below.

No.

Value

Keyword

Source

Remark

1

\(a_1 = \ldots = a_M = 0\)

Saltelli1995-1

[SSobol95] (Example 1) (also [BFN92])

All input variables are equally important

2

\(a_1 = a_2 = 0\)
\(a_3 = 3\)
\(a_3 = \ldots = a_M = 9\)

Saltelli1995-2

[SSobol95] (Example 2)

The first two are important, the next is moderately important, and the rest is non-influential

3

\(a_m = \frac{m - 1}{2.0}\)
\(1 \leq m \leq M\)

Saltelli1995-3 (default)

[SSobol95] (Example 3) (also [CMLML07] )

The most important input is the first one, the least is the last one

4

\(a_1 = \ldots = a_M = 0.01\)

Sobol1998-1

[Sobol98] (choice 1)

The supremum of the function grows exponentially at \(2^M\)

5

\(a_1 = \ldots = a_M = 1.0\)

Sobol1998-2

[Sobol98] (choice 2)

The supremum of the function grows exponentially at \(1.5^M\)

6

\(a_m = m\)
\(\, 1 \leq m \leq M\)

Sobol1998-3

[Sobol98] (choice 3)

The supremum of the function grows linearly at \(1 + \frac{M}{2}\)

7

\(a_m = m^2\)
\(1 \leq m \leq M\)

Sobol1998-4

[Sobol98] (choice 4)

The supremum is bounded at \(1.0\)

8

\(a_1 = a_2 = 0.0\)
\(a_3 = \ldots = a_M = 6.52\)

Kucherenko2011-2a

[KFSM11] (Problem 2A)

Originally, \(M = 100\)

9

\(a_m = 6,52\)
\(1 \leq m \leq M\)

Kucherenko2011-3b

[KFSM11] (Problem 3B)

Note

The parameter values used in [MIVDV08] and [MILR09] correspond to the parameter choice 3 in [Sobol98].

Note

To create an instance of the Sobol’-G function with different built-in parameter values, pass the corresponding keyword to the parameter parameters_selection. For example, to use the parameters of problem 3B from [KFSM11], type:

my_testfun = uqtf.SobolG(parameters_selection="Kucherenko2011-3b")

Reference results#

This section provides several reference results of typical UQ analyses involving the test function.

Sample histogram#

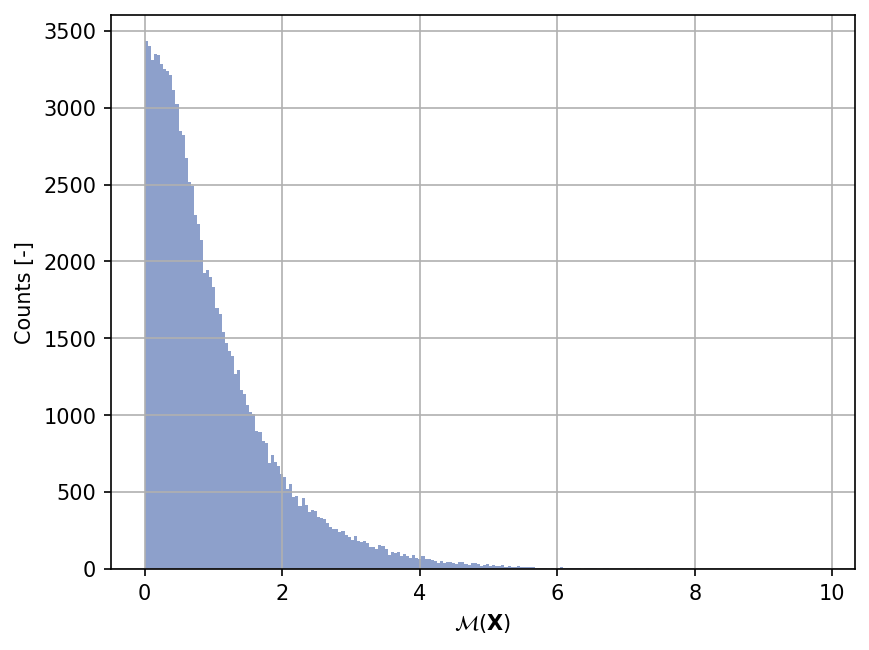
Shown below is the histogram of the output based on \(100'000\) random points:

np.random.seed(42)
xx_test = my_testfun.prob_input.get_sample(100000)
yy_test = my_testfun(xx_test)

plt.hist(yy_test, bins="auto", color="#8da0cb");
plt.grid();
plt.ylabel("Counts [-]");
plt.xlabel("$\mathcal{M}(\mathbf{X})$");
plt.gcf().set_dpi(150);
../_images/sobol-g_13_0.png

Definite integration#

The integral value of the function over the whole domain \([0, 1]^M\) is analytical:

\[ \int_{[0, 1]^M} \mathcal{M}(\boldsymbol{x}) \; d\boldsymbol{x} = 1.0. \]

Moments estimation#

The mean and variance of the Sobol’-G function can be computed analytically,
and the results are:

  • \(\mathbb{E}[Y] = 1.0\)3

  • \(\mathbb{V}[Y] = \prod_{m = 1}^{M} \frac{\frac{4}{3} + 2 a_m + a_m^2}{(1 + a_m)^2} - 1\)

Notice that the values of these two moments depend on the choice of the parameter values.

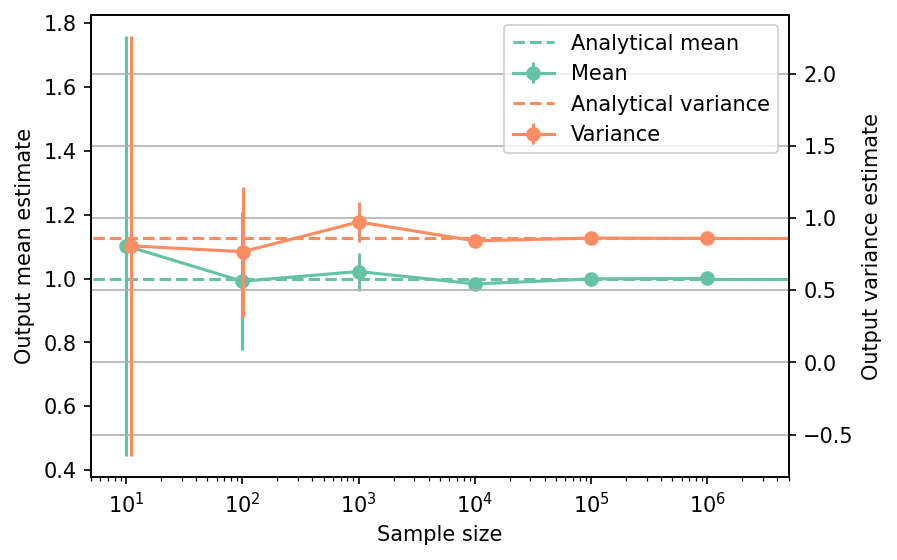
Shown below is the convergence of a direct Monte-Carlo estimation of the output mean and variance with increasing sample sizes compared with the analytical values. The error bars corresponds to twice the standard deviation of the estimates obtained from \(50\) replications.

# --- Compute the mean and variance estimate
np.random.seed(42)
sample_sizes = np.array([1e1, 1e2, 1e3, 1e4, 1e5, 1e6], dtype=int)
mean_estimates = np.empty((len(sample_sizes), 50))
var_estimates = np.empty((len(sample_sizes), 50))

for i, sample_size in enumerate(sample_sizes):
    for j in range(50):
        xx_test = my_testfun.prob_input.get_sample(sample_size)
        yy_test = my_testfun(xx_test)
        mean_estimates[i, j] = np.mean(yy_test)
        var_estimates[i, j] = np.var(yy_test)

mean_estimates_errors = np.std(mean_estimates, axis=1)
var_estimates_errors = np.std(var_estimates, axis=1)

# --- Compute analytical mean and variance
params = my_testfun.parameters
mean_analytical = 1.0
var_analytical = np.prod((4 / 3 + 2 * params + params**2) / (1 + params)**2) - 1

# --- Plot the mean and variance estimates
fig, ax_1 = plt.subplots(figsize=(6,4))

ext_sample_sizes = np.insert(sample_sizes, 0, 1)
ext_sample_sizes = np.insert(ext_sample_sizes, -1, 5e6)

# --- Mean plot
ax_1.errorbar(
    sample_sizes,
    mean_estimates[:,0],
    yerr=2.0*mean_estimates_errors,
    marker="o",
    color="#66c2a5",
    label="Mean"
)
# Plot the analytical mean
ax_1.plot(
    ext_sample_sizes,
    np.repeat(mean_analytical, len(ext_sample_sizes)),
    linestyle="--",
    color="#66c2a5",
    label="Analytical mean",
)
ax_1.set_xlim([5, 5e6])
ax_1.set_xlabel("Sample size")
ax_1.set_ylabel("Output mean estimate")
ax_1.set_xscale("log");
ax_2 = ax_1.twinx()

# --- Variance plot
ax_2.errorbar(
    sample_sizes+1,
    var_estimates[:,0],
    yerr=2.0*var_estimates_errors,
    marker="o",
    color="#fc8d62",
    label="Variance",
)
# Plot the analytical variance
ax_2.plot(
    ext_sample_sizes,
    np.repeat(var_analytical, len(ext_sample_sizes)),
    linestyle="--",
    color="#fc8d62",
    label="Analytical variance",
)
ax_2.set_ylabel("Output variance estimate")

# Add the two plots together to have a common legend
ln_1, labels_1 = ax_1.get_legend_handles_labels()
ln_2, labels_2 = ax_2.get_legend_handles_labels()
ax_2.legend(ln_1 + ln_2, labels_1 + labels_2, loc=0)

plt.grid()
fig.set_dpi(150)
../_images/sobol-g_15_0.png

The tabulated results for each sample size is shown below.

from tabulate import tabulate

# --- Compile data row-wise
outputs = [
    [
        np.nan,
        mean_analytical,
        0.0,
        var_analytical,
        0.0,
        "Analytical",
    ]
]

for (
    sample_size,
    mean_estimate,
    mean_estimate_error,
    var_estimate,
    var_estimate_error,
) in zip(
    sample_sizes,
    mean_estimates[:,0],
    2.0*mean_estimates_errors,
    var_estimates[:,0],
    2.0*var_estimates_errors,
):
    outputs += [
        [
            sample_size,
            mean_estimate,
            mean_estimate_error,
            var_estimate,
            var_estimate_error,
            "Monte-Carlo",
        ],
    ]

header_names = [
    "Sample size",
    "Mean",
    "Mean error",
    "Variance",
    "Variance error",
    "Remark",
]

tabulate(
    outputs,
    numalign="center",
    stralign="center",
    tablefmt="html",
    floatfmt=(".1e", ".4e", ".4e", ".4e", ".4e", "s"),
    headers=header_names
)
Sample size Mean Mean error Variance Variance error Remark
nan 1.0000e+00 0.0000e+00 8.6088e-01 0.0000e+00 Analytical
1.0e+01 1.1024e+00 6.5742e-01 8.0829e-01 1.4564e+00 Monte-Carlo
1.0e+02 9.9178e-01 2.1635e-01 7.6833e-01 4.5027e-01 Monte-Carlo
1.0e+03 1.0222e+00 5.9467e-02 9.7429e-01 1.4066e-01 Monte-Carlo
1.0e+04 9.8333e-01 1.7392e-02 8.4345e-01 4.6349e-02 Monte-Carlo
1.0e+05 9.9906e-01 4.9575e-03 8.6216e-01 1.4366e-02 Monte-Carlo
1.0e+06 1.0006e+00 1.9133e-03 8.6021e-01 4.8536e-03 Monte-Carlo

References#

SSobol95(1,2,3,4)

Andrea Saltelli and Ilya M. Sobol'. About the use of rank transformation in sensitivity analysis of model output. Reliability Engineering & System Safety, 50(3):225–239, 1995. doi:10.1016/0951-8320(95)00099-2.

BFN92

Paul Bratley, Bennett L. Fox, and Harald Niederreiter. Implementation and tests of low-discrepancy sequences. ACM Transactions on Modeling and Computer Simulation, 2(3):195–213, 1992. doi:10.1145/146382.146385.

MILR09(1,2)

Amandine Marrel, Bertrand Iooss, Béatrice Laurent, and Olivier Roustant. Calculations of Sobol indices for the Gaussian process metamodel. Reliability Engineering & System Safety, 94(3):742–751, 2009. doi:10.1016/j.ress.2008.07.008.

RSobolT96

Igor Radović, Ilya M. Sobol', and Robert F. Tichy. Quasi-Monte Carlo methods for numerical integration: comparison of different low discrepancy sequences. Monte Carlo Methods and Applications, 2(1):1–14, 1996. doi:10.1515/mcma.1996.2.1.1.

Sobol98(1,2,3,4,5,6,7)

Ilya M. Sobol'. On quasi-Monte Carlo integrations. Mathematics and Computers in Simulation, 47(2-5):103–112, 1998. doi:10.1016/s0378-4754(98)00096-2.

MIVDV08(1,2)

Amandine Marrel, Bertrand Iooss, François Van Dorpe, and Elena Volkova. An efficient methodology for modeling complex computer codes with Gaussian processes. Computational Statistics & Data Analysis, 52(10):4731–4744, 2008. doi:10.1016/j.csda.2008.03.026.

KFSM11(1,2,3,4)

Sergei Kucherenko, Balazs Feil, Nilay Shah, and Wolfgang Mauntz. The identification of model effective dimensions using global sensitivity analysis. Reliability Engineering & System Safety, 96(4):440–449, 2011. doi:10.1016/j.ress.2010.11.003.

CMLML07

Thierry Crestaux, Jean-Marc Martinez, Olivier Le Maître, and Olivier Lafitte. Polynomial chaos expansion for uncertainties quantification and sensitivity analysis. Presented at the Fifth International Conference on Sensitivity Analysis of Model Output, 2007. URL: http://samo2007.chem.elte.hu/lectures/Crestaux.pdf.

1

This default dimension applies to all variable dimension test functions. It will be used if the spatial_dimension argument is not given.

2

see Eqs. (23) and (24), p. 234 in [SSobol95].

3

The expected value is the same as the integral over the domain because the input is uniform in a unit hypercube.