Twenty-dimensional Function from Alemazkoor and Meidani (2018)

Twenty-dimensional Function from Alemazkoor and Meidani (2018)#

import numpy as np
import matplotlib.pyplot as plt
import uqtestfuns as uqtf

The 20-dimensional test function from [AM18] (or Alemazkoor20D for short) is a polynomial function that features low-degree of interactions (i.e., \(2\)) between the input variables (i.e., high in dimension but of low-degree). It was used as a test function for a metamodeling exercise (i.e., sparse polynomial chaos expansion).

Test function instance#

To create a default instance of the Alemazkoor20D function1:

my_testfun = uqtf.Alemazkoor20D()

Check if it has been correctly instantiated:

print(my_testfun)

Name              : Alemazkoor20D
Spatial dimension : 20
Description       : High-dimensional low-degree polynomial from Alemazkoor & Meidani (2018)

Description#

The Alemazkoor20D function is defined as follows:

\[ \mathcal{M}(\boldsymbol{x}) = \sum_{i = 1}^{19} x_{i} x_{i+1} \]

where \(\boldsymbol{x} = \{ x_1, \ldots, x_{20} \}\) is the twenty-dimensional vector of input variables further defined below.

Probabilistic input#

Based on [AM18], the probabilistic input model for the function consists of twenty independent random variables as shown in the table below.

No.	Name	Distribution	Parameters	Description
1	\(x_1\)	uniform	[-1.0, 1.0]	N/A
\(\vdots\)	\(\vdots\)	\(\vdots\)	\(\vdots\)	\(\vdots\)
20	\(x_{20}\)	uniform	[-1.0, 1.0]	N/A

Reference results#

This section provides several reference results of typical UQ analyses involving the test function.

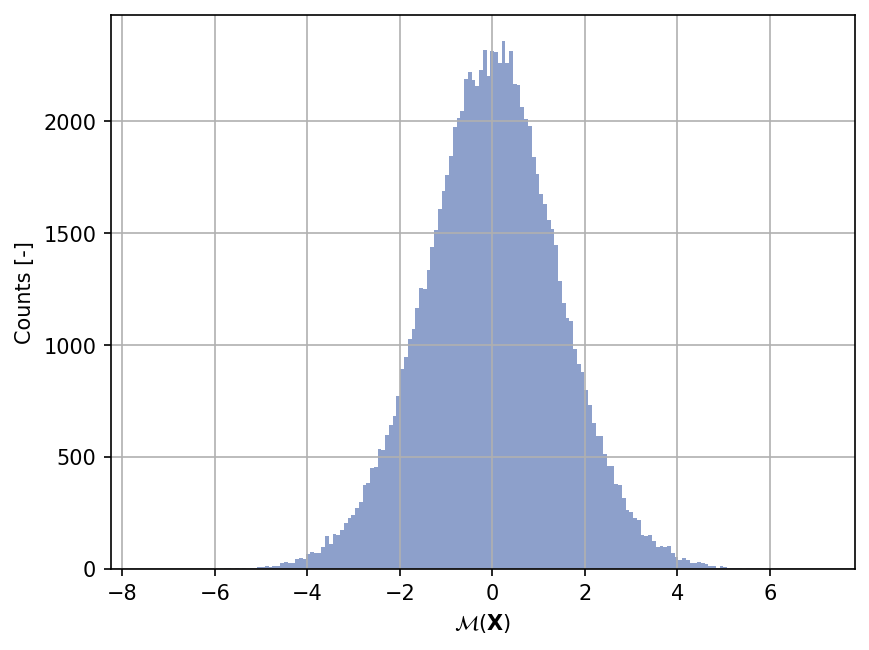
Sample histogram#

Shown below is the histogram of the output based on \(100'000\) random points:

xx_test = my_testfun.prob_input.get_sample(100000)
yy_test = my_testfun(xx_test)

plt.hist(yy_test, bins="auto", color="#8da0cb");
plt.grid();
plt.ylabel("Counts [-]");
plt.xlabel("$\mathcal{M}(\mathbf{X})$");
plt.gcf().set_dpi(150);

References#

AM18(1,2,3): Negin Alemazkoor and Hadi Meidani. A near-optimal sampling strategy for sparse recovery of polynomial chaos expansions. Journal of Computational Physics, 371:137–151, 2018. doi:10.1016/j.jcp.2018.05.025.

1: see Section 4.1, Eq. (32) in [AM18].

UQTestFuns